Article contents
The influence of a small upstream wire on transition in a rotating cylinder wake
Published online by Cambridge University Press: 25 March 2015
Abstract
Recent experimental research on rotating cylinder wakes has found that a previously numerically predicted subharmonic instability mode, mode C, occurs for considerably lower rotation rates than predicted through stability analysis, yet other mode transitions occur closer to the predicted onset. One difference between the theoretical and experimental set-ups is the use of a small-diameter hydrogen bubble visualisation wire placed upstream of the rotating cylinder. The current paper tests the hypothesis that a wire, of only 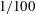 $1/100$ th of the cylinder diameter, placed five diameters upstream of the cylinder, sufficiently perturbs the flow to substantially affect certain wake transitions, including the onset of mode C. This is achieved using stability analysis of a flow that includes the upstream wire. The results indeed show that the wire of a tiny diameter induces a non-negligible asymmetry in the flow, triggering the subharmonic mode at substantially lower rotation rates. Furthermore, at higher rotation rates, the onset of two other three-dimensional modes are delayed to higher Reynolds numbers. These results make the point that even seemingly minute perturbations caused by minimally intrusive methods may result in substantially altered experimental flow behaviour.
$1/100$ th of the cylinder diameter, placed five diameters upstream of the cylinder, sufficiently perturbs the flow to substantially affect certain wake transitions, including the onset of mode C. This is achieved using stability analysis of a flow that includes the upstream wire. The results indeed show that the wire of a tiny diameter induces a non-negligible asymmetry in the flow, triggering the subharmonic mode at substantially lower rotation rates. Furthermore, at higher rotation rates, the onset of two other three-dimensional modes are delayed to higher Reynolds numbers. These results make the point that even seemingly minute perturbations caused by minimally intrusive methods may result in substantially altered experimental flow behaviour.
JFM classification
Information
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 7
- Cited by

