Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-26T22:12:22.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial rise of a meniscus on a vertical cylinder

Published online by Cambridge University Press:  03 March 2015

Doireann O’Kiely ,
Jonathan P. Whiteley ,
James M. Oliver  and
Dominic Vella
Doireann O’Kiely
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
Jonathan P. Whiteley
Affiliation:
Department of Computer Science, University of Oxford, Wolfson Building, Parks Road, Oxford OX1 3QD, UK
James M. Oliver
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
Dominic Vella*
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, UK
*
†Email address for correspondence: dominic.vella@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the inertia-dominated rise of a meniscus around a vertical circular cylinder. Previous experiments and scaling analysis suggest that the height of the meniscus, 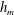$h_{m}$, grows with the time following the initiation of rise, $t$, like 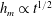$h_{m}\propto t^{1/2}$. This is in contrast to the rise on a vertical plate, which obeys the classic capillary–inertia scaling 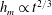$h_{m}\propto t^{2/3}$. We highlight a subtlety in the scaling analysis that yielded 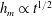$h_{m}\propto t^{1/2}$ and investigate the consequences of this subtlety. We develop a potential flow model of the dynamic problem, which we solve using the finite element method. Our numerical results agree well with previous experiments but suggest that the correct early time behaviour is, in fact, 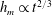$h_{m}\propto t^{2/3}$. Furthermore, we show that at intermediate times the dynamic rise of the meniscus is governed by two parameters: the contact angle and the cylinder radius measured relative to the capillary length scale, 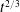$t^{2/3}$. This result allows us to collapse previous experimental results with different cylinder radii (but similar static contact angles) onto a single master curve.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , R2
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablett, R. 1923 An investigation of the angle of contact between paraffin wax and water. Phil. Mag. 46, 244–256.CrossRefGoogle Scholar
Billingham, J. & King, A. C. 1995 The interaction of a moving fluid fluid interface with a flat plate. J. Fluid Mech. 296, 325–357.CrossRefGoogle Scholar
Bush, J. W. M. & Hu, D. L. 2006 Walking on water: biolocomotion at the interface. Annu. Rev. Fluid Mech. 38, 339–369.CrossRefGoogle Scholar
Clanet, C. & Quéré, D. 2002 Onset of menisci. J. Fluid Mech. 460, 131–149.CrossRefGoogle Scholar
Duchemin, L., Eggers, J. & Josserand, C. 2003 Inviscid coalescence of drops. J. Fluid Mech. 487, 167–178.CrossRefGoogle Scholar
Duchemin, L. & Vandenberghe, N. 2014 Impact dynamics for a floating elastic membrane. J. Fluid Mech. 756, 544–554.CrossRefGoogle Scholar
Eriksson, K., Estep, D., Hansbo, P. & Johnson, C. 1996 Computational Differential Equations. Cambridge University Press.Google Scholar
Finn, R. 1986 Equilibrium Capillary Surfaces. Springer.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Howison, S. D., Morgan, J. D. & Ockendon, J. R. 1997 A class of codimension-two free boundary problems. SIAM Rev. 39 (2), 221–253.CrossRefGoogle Scholar
Hu, D. L. & Bush, J. W. M. 2005 Meniscus-climbing insects. Nature 437, 733–736.CrossRefGoogle ScholarPubMed
James, D. F. 1974 The meniscus on the outside of a small circular cylinder. J. Fluid Mech. 63 (4), 657–664.CrossRefGoogle Scholar
Keller, J. B. & Miksis, M. J. 1983 Surface tension driven flows. SIAM J. Appl. Maths 43 (2), 268–277.CrossRefGoogle Scholar
King, J. R., Ockendon, J. R. & Ockendon, H. 1999 The Laplace–Young equation near a corner. Q. J. Mech. Appl. Maths 52, 73–97.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, Course of Theoretical Physics, vol. 6. Butterworth-Heinemann.Google Scholar
Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15, 568–578.CrossRefGoogle Scholar
Lo, L. L. 1983 The meniscus on a needle – a lesson in matching. J. Fluid Mech. 132 (1), 65–78.CrossRefGoogle Scholar
Ponomarenko, A., Quéré, D. & Clanet, C. 2011 A universal law for capillary rise in corners. J. Fluid Mech. 666, 146–154.CrossRefGoogle Scholar
Quéré, D. 1997 Inertial capillarity. Europhys. Lett. 39, 533–538.CrossRefGoogle Scholar
Reyssat, M., Courbin, L., Reyssat, E. & Stone, H. A. 2008 Imbibition in geometries with axial variations. J. Fluid Mech. 615, 335–344.CrossRefGoogle Scholar
Sierou, A. & Lister, J. R. 2004 Self-similar recoil of inviscid drops. Phys. Fluids 16, 1379–1394.CrossRefGoogle Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Thompson, A. B. & Billingham, J. 2012 Inviscid coalescence in the presence of a surrounding fluid. IMA J. Appl. Maths 77 (5), 678–696.CrossRefGoogle Scholar
Vella, D., Lee, D.-G. & Kim, H.-Y. 2006 Sinking of a horizontal cylinder. Langmuir 22, 2972–2974.CrossRefGoogle ScholarPubMed
Vella, D. & Li, J. 2010 The impulsive motion of a small cylinder at an interface. Phys. Fluids 22, 052104.CrossRefGoogle Scholar
Vella, D. & Metcalfe, P. D. 2007 Surface tension dominated impact. Phys. Fluids 19, 072108.CrossRefGoogle Scholar
Washburn, E. W. 1921 The dynamics of capillary flow. Phys. Rev. 17, 273–283.CrossRefGoogle Scholar
Young, T. 1805 An essay on the cohesion of fluids. Phil. Trans. R. Soc. 95, 65–87.Google Scholar