Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Petter, Samuel J.
Lynch, Kyle P.
Farias, Paul
Spitzer, Seth
Grasser, Thomas
and
Wagner, Justin L.
2020.
Early Experiments on Shock-Particle Interactions in the High-Temperature Shock Tube.
Shallcross, Gregory S.
Fox, Rodney O.
and
Capecelatro, Jesse
2020.
A volume-filtered description of compressible particle-laden flows.
International Journal of Multiphase Flow,
Vol. 122,
Issue. ,
p.
103138.
Daniel, Kyle
Farias, Paul
and
Wagner, Justin L.
2021.
The Shock-Induced Disperal of Dense Particle Curtains with Varying Density.
Ren, Yi
Shen, Yi
Wang, Pei
and
Ding, Hang
2021.
Simulation of interaction between shocks and particle cloud using a second-order conservative sharp interface method.
Journal of Computational Physics,
Vol. 439,
Issue. ,
p.
110410.
Li, Jiarui
Xue, Kun
Zeng, Junsheng
Tian, Baolin
and
Guo, Xiaohu
2022.
Shock-induced interfacial instabilities of granular media.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Daniel, Kyle A.
and
Wagner, Justin L.
2022.
The shock-induced dispersal of particle curtains with varying material density.
International Journal of Multiphase Flow,
Vol. 152,
Issue. ,
p.
104082.
Jiang, Ling-Jie
and
Li, Maojun
2022.
Particle-resolved simulations of shock-induced inviscid flow through particle-curtain at initial stage.
Computers & Fluids,
Vol. 232,
Issue. ,
p.
105196.
DeChant, Lawrence J.
Daniel, Kyle
Wagner, Justin L.
and
Teeter, Russell
2023.
Shock Induced Particle Curtain Dispersion: Asymptotic Drag Law Scaling Formulations and Relationship to Streamwise Pressure Difference Models.
Wagner, Justin L.
Daniel, Kyle
Downing, Charley
Grasser, Thomas W.
and
Lynch, Kyle P.
2023.
Shock-Particle Curtain Interactions at High Mach Number.
Boniou, Victor
and
Fox, Rodney O.
2023.
Shock-Particle-Interaction Study with a Hyperbolic Two-Fluid Model.
SSRN Electronic Journal,
2023.
Coarse-grained numerical simulation for compressible fluid–particle two-phase flows.
Physics of Fluids,
Vol. 35,
Issue. 5,
Zhang, Pikai
Zhang, Huangwei
Zhang, Yun Feng
Li, Shangpeng
and
Meng, Qingyang
2023.
Modeling particle collisions in moderately dense curtain impacted by an incident shock wave.
Physics of Fluids,
Vol. 35,
Issue. 2,
Zhang, Lite
Feng, Zilong
Sun, Mengyu
Guan, Hao
Jin, Haozhe
and
Shi, Honghui
2023.
Modeling of long-term shock interaction with a movable particle curtain in a rectangular tube based on a dense discrete phase model.
Powder Technology,
Vol. 415,
Issue. ,
p.
118116.
Gessman, Isabella
Murzyn, Christopher
Swain, Will E.
Downing, Charley
and
Daniel, Kyle
2024.
Optical Pressure Measurements via Water Vapor Absorption Spectroscopy in a Shock Tube.
Chen, Feiguo
and
Ge, Wei
2024.
General drag correlations for subsonic to supersonic flow past ordered particle arrays at low and moderate Reynolds numbers.
Computers & Fluids,
Vol. 278,
Issue. ,
p.
106324.
Wu, Qi
Meng, Baoqing
Zhang, Yousheng
Shi, Yipeng
and
Tian, Baolin
2024.
Proceedings of the IUTAM Symposium on Turbulent Structure and Particles-Turbulence Interaction.
Vol. 41,
Issue. ,
p.
326.
Lai, S.
Rao, Y.
and
Wang, H.
2024.
Computational analysis of a dense granular system driven by a propagating shock wave in an Eulerian–Eulerian framework.
Physics of Fluids,
Vol. 36,
Issue. 4,
Capecelatro, Jesse
and
Wagner, Justin L.
2024.
Gas–Particle Dynamics in High-Speed Flows.
Annual Review of Fluid Mechanics,
Vol. 56,
Issue. 1,
p.
379.
Wu, Qi
Zhang, Yousheng
Meng, Baoqing
Shi, Yipeng
and
Tian, Baolin
2024.
Freeze out of multi-mode Richtmyer–Meshkov instability using particles.
Physics of Fluids,
Vol. 36,
Issue. 6,
Hsiao, Smyther S.
Ouellet, Frederick
and
Regele, Jonathan D.
2025.
Generalizing the compressible pairwise interaction extended point-particle model.
Physica D: Nonlinear Phenomena,
Vol. 482,
Issue. ,
p.
134907.
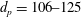 $d_{p}=106{-}125$,
$d_{p}=106{-}125$, 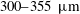 $300{-}355~\unicode[STIX]{x03BC}\text{m}$) across Mach numbers ranging from 1.24 to 2.02. Using these data, along with data compiled from the literature, the dispersion of a dense curtain was studied for multiple Mach numbers (1.2–2.6), particle sizes (
$300{-}355~\unicode[STIX]{x03BC}\text{m}$) across Mach numbers ranging from 1.24 to 2.02. Using these data, along with data compiled from the literature, the dispersion of a dense curtain was studied for multiple Mach numbers (1.2–2.6), particle sizes (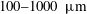 $100{-}1000~\unicode[STIX]{x03BC}\text{m}$) and volume fractions (9–32 %). Data were non-dimensionalized according to two different scaling methods found within the literature, with time scales defined based on either particle propagation time or pressure ratio across a reflected shock. The data show that spreading of the particle curtain is a function of the volume fraction, with the effectiveness of each time scale based on the proximity of a given curtain’s volume fraction to the dilute mixture regime. It is seen that volume fraction corrections applied to a traditional particle propagation time scale result in the best collapse of the data between the two time scales tested here. In addition, a constant-thickness regime has been identified, which has not been noted within previous literature.
$100{-}1000~\unicode[STIX]{x03BC}\text{m}$) and volume fractions (9–32 %). Data were non-dimensionalized according to two different scaling methods found within the literature, with time scales defined based on either particle propagation time or pressure ratio across a reflected shock. The data show that spreading of the particle curtain is a function of the volume fraction, with the effectiveness of each time scale based on the proximity of a given curtain’s volume fraction to the dilute mixture regime. It is seen that volume fraction corrections applied to a traditional particle propagation time scale result in the best collapse of the data between the two time scales tested here. In addition, a constant-thickness regime has been identified, which has not been noted within previous literature.
