Article contents
The impact of a deep-water plunging breaker on a wall with its bottom edge close to the mean water surface
Published online by Cambridge University Press: 04 April 2018
Abstract
The impact of a deep-water plunging breaker on a finite height two-dimensional structure with a vertical front face is studied experimentally. The structure is located at a fixed horizontal position relative to a wave maker and the structure’s bottom surface is located at a range of vertical positions close to the undisturbed water surface. Measurements of the water surface profile history and the pressure distribution on the front surface of the structure are performed. As the vertical position, 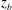 $z_{b}$ (the
$z_{b}$ (the  $z$ axis is positive up and
$z$ axis is positive up and 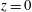 $z=0$ is the mean water level), of the structure’s bottom surface is varied from one experimental run to another, the water surface evolution during impact can be categorized into three classes of behaviour. In class I, with
$z=0$ is the mean water level), of the structure’s bottom surface is varied from one experimental run to another, the water surface evolution during impact can be categorized into three classes of behaviour. In class I, with 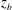 $z_{b}$ in a range of values near
$z_{b}$ in a range of values near 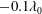 $-0.1\unicode[STIX]{x1D706}_{0}$, where
$-0.1\unicode[STIX]{x1D706}_{0}$, where 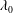 $\unicode[STIX]{x1D706}_{0}$ is the nominal wavelength of the breaker, the behaviour of the water surface is similar to the flip-through phenomena first described in studies with shallow water and a structure mounted on the sea bed. In the present work, it is found that the water surface between the front face of the structure and the wave crest is well fitted by arcs of circles with a decreasing radius and downward moving centre as the impact proceeds. A spatially and temporally localized high-pressure region was found on the impact surface of the structure and existing theory is used to explore the physics of this phenomenon. In class II, with
$\unicode[STIX]{x1D706}_{0}$ is the nominal wavelength of the breaker, the behaviour of the water surface is similar to the flip-through phenomena first described in studies with shallow water and a structure mounted on the sea bed. In the present work, it is found that the water surface between the front face of the structure and the wave crest is well fitted by arcs of circles with a decreasing radius and downward moving centre as the impact proceeds. A spatially and temporally localized high-pressure region was found on the impact surface of the structure and existing theory is used to explore the physics of this phenomenon. In class II, with 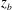 $z_{b}$ in a range of values near the mean water level, the bottom of the structure exits and re-enters the water phase at least once during the impact process. These air–water transitions generate large-amplitude ripple packets that propagate to the wave crest and modify its behaviour significantly. At
$z_{b}$ in a range of values near the mean water level, the bottom of the structure exits and re-enters the water phase at least once during the impact process. These air–water transitions generate large-amplitude ripple packets that propagate to the wave crest and modify its behaviour significantly. At 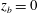 $z_{b}=0$, all sensors submerged during the impact record a nearly in-phase high-frequency pressure oscillation indicating possible air entrainment. In class III, with
$z_{b}=0$, all sensors submerged during the impact record a nearly in-phase high-frequency pressure oscillation indicating possible air entrainment. In class III, with 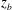 $z_{b}$ in a range of values near
$z_{b}$ in a range of values near 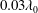 $0.03\unicode[STIX]{x1D706}_{0}$, the bottom of the structure remains in air before the main crest hits the bottom corner of the structure. The subsequent free surface behaviour is strongly influenced by the instantaneous momentum of the local flow just before impact and the highest wall pressures of all experimental conditions are found.
$0.03\unicode[STIX]{x1D706}_{0}$, the bottom of the structure remains in air before the main crest hits the bottom corner of the structure. The subsequent free surface behaviour is strongly influenced by the instantaneous momentum of the local flow just before impact and the highest wall pressures of all experimental conditions are found.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: Kevin T. Crofton Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24061, USA.
References
Wang et al. supplementary movie 1
LIF high-speed movie of the breaker in open water (corresponding to figure 4).
Wang et al. supplementary movie 2
LIF high-speed movie of the water surface profile for $z_b = -0.113\lambda_0$ (corresponding to figure 5).
Wang et al. supplementary movie 3
LIF high-speed movie of the water surface profile for $z_b = 0$ (corresponding to figure 9).
Wang et al. supplementary movie 4
LIF high-speed movie of the water surface profile for $z_b = 0.022\lambda_0$ (corresponding to figure 13).
- 9
- Cited by

