Article contents
Hysteresis phenomena in gravity–capillary waves on deep water generated by a moving two-dimensional/three-dimensional air-blowing/air-suction forcing
Published online by Cambridge University Press: 23 December 2019
Abstract
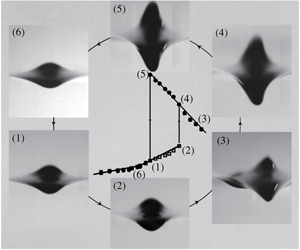
Hysteresis phenomena in forced gravity–capillary waves on deep water where the minimum phase speed  $c_{min}=23~\text{cm}~\text{s}^{-1}$ are experimentally investigated. Four kinds of forcings are considered: two-dimensional/three-dimensional air-blowing/air-suction forcings. For a still-water initial condition, as the forcing speed increases from zero towards a certain target speed (
$c_{min}=23~\text{cm}~\text{s}^{-1}$ are experimentally investigated. Four kinds of forcings are considered: two-dimensional/three-dimensional air-blowing/air-suction forcings. For a still-water initial condition, as the forcing speed increases from zero towards a certain target speed ( $U$), there exists a certain critical speed (
$U$), there exists a certain critical speed ( $U_{crit}$) at which the transition from linear to nonlinear states occurs. When
$U_{crit}$) at which the transition from linear to nonlinear states occurs. When  $U<U_{crit}$, steady linear localized waves are observed (state I). When
$U<U_{crit}$, steady linear localized waves are observed (state I). When  $U_{crit}<U<c_{min}$, steady nonlinear localized waves, including steep gravity–capillary solitary waves, are observed (state II). When
$U_{crit}<U<c_{min}$, steady nonlinear localized waves, including steep gravity–capillary solitary waves, are observed (state II). When  $U\approx c_{min}$, periodic shedding phenomena of nonlinear localized depressions are observed (state III). When
$U\approx c_{min}$, periodic shedding phenomena of nonlinear localized depressions are observed (state III). When  $U>c_{min}$, steady linear non-local waves are observed (state IV). Next, with these state-II, III and IV waves as new initial conditions, as the forcing speed is decreased towards a certain target speed (
$U>c_{min}$, steady linear non-local waves are observed (state IV). Next, with these state-II, III and IV waves as new initial conditions, as the forcing speed is decreased towards a certain target speed ( $U_{final}$), a certain critical speed (
$U_{final}$), a certain critical speed ( $U_{crit,2}$) is identified at which the transition from nonlinear to linear states occurs. When
$U_{crit,2}$) is identified at which the transition from nonlinear to linear states occurs. When  $U_{crit,2}<U_{final}<U_{crit}$, relatively steeper steady nonlinear localized waves, including steeper gravity–capillary solitary waves, are observed. When
$U_{crit,2}<U_{final}<U_{crit}$, relatively steeper steady nonlinear localized waves, including steeper gravity–capillary solitary waves, are observed. When  $U_{final}<U_{crit,2}$, linear state-I waves are observed. These are hysteresis phenomena, which show jump transitions from linear to nonlinear states and from nonlinear to linear states at two different critical speeds. For air-blowing cases, experimental results are compared with simulation results based on a theoretical model equation. They agree with each other very well except that the experimentally identified critical speed (
$U_{final}<U_{crit,2}$, linear state-I waves are observed. These are hysteresis phenomena, which show jump transitions from linear to nonlinear states and from nonlinear to linear states at two different critical speeds. For air-blowing cases, experimental results are compared with simulation results based on a theoretical model equation. They agree with each other very well except that the experimentally identified critical speed ( $U_{crit,2}$) is different from the theoretically predicted one.
$U_{crit,2}$) is different from the theoretically predicted one.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 2
- Cited by

