1. Introduction
Swimming droplets are artificial micro-swimmers that are driven by an asymmetric distribution of external energy sources across the interface (Maass et al. Reference Maass, Krúger, Herminghaus and Bahr2016; Weber et al. Reference Weber, Zwicker, Jülicher and Lee2019). These systems are of tremendous interest as experimental models for mimicking the motion of several biological systems (Čejková et al. Reference Čejková, Banno, Hanczyc and Štěpánek2017; Li et al. Reference Li, Brinkmann, Pagonabarraga, Seemann and Fleury2018). For most motile biological systems, the necessary isotropic symmetry breaking for propulsion occurs intrinsically, i.e. through the beating of the associated appendages cilia or flagella (Lauga & Powers Reference Lauga and Powers2009) or due to shape deformation (D'Ambrosio & Sinigaglia Reference D'Ambrosio, Sinigaglia, D'Ambrosio and Sinigaglia2003). However, for droplets, typically the swimmer itself is perfectly isotropic, and the associated symmetry is broken through the external energy sources (Herminghaus et al. Reference Herminghaus, Maass, Kruger, Thutupalli, Goehring and Bahr2014; Yoshinaga Reference Yoshinaga2017). In the literature, the propulsion mechanisms of several external sources are believed to be reasonably well understood (Saintillan & Shelley Reference Saintillan, Shelley and Spagnolie2015; Seemann, Fleury & Maass Reference Seemann, Fleury and Maass2016; Kree, Burada & Zippelius Reference Kree, Burada and Zippelius2017). Theoretical as well as numerical studies have considered droplets in a chemically reacting fluid (Kitahata et al. Reference Kitahata, Yoshinaga, Nagai and Sumino2011; Thutupalli & Herminghaus Reference Thutupalli and Herminghaus2011; Fadda et al. Reference Fadda, Gonnella, Lamura and Tiribocchi2017), in an inhomogeneous temperature field (Subramanian Reference Subramanian1992; Karbalaei, Kumar & Cho Reference Karbalaei, Kumar and Cho2016) or droplets that move owing to liquid–liquid phase separation (Lamorgese & Mauri Reference Lamorgese and Mauri2011, Reference Lamorgese and Mauri2017) etc. In particular, active droplets driven by nonlinear advection effects of the surfactants (Furtado, Pooley & Yeomans Reference Furtado, Pooley and Yeomans2008; Mozorov & Michelin Reference Mozorov and Michelin2019) or the thermal field (Balasubramaniam & Subramanian Reference Balasubramaniam and Subramanian2000; Zhang, Subramanian & Balasubramaniam Reference Zhang, Subramanian and Balasubramaniam2001) and surfactant-stabilized droplets driven by solubilization (Pena & Miller Reference Pena and Miller2006; Ariyaprakai & Dungan Reference Ariyaprakai and Dungan2008) have gained significant attention in the last decade.
All the sources, as mentioned earlier, cause the interface tension of the droplet to vary along the surface. This phenomenon is known as the Marangoni effect (Scriven & Sternling Reference Scriven and Sternling1960; Lauga & Davis Reference Lauga and Davis2012). There exist extensive studies for the flow field around a Marangoni-driven active droplet in the quasi-steady Stokesian regime (Schmitt & Stark Reference Schmitt and Stark2013, Reference Schmitt and Stark2016a,Reference Schmitt and Starkb; Masoud & Stone Reference Masoud and Stone2014; Stricker Reference Stricker2017) neglecting the inertial effect. Inertial swimming within the context of biological systems serves as a useful tool in several scientific applications (Reynolds Reference Reynolds1965; Hamel et al. Reference Hamel, Fisch, Combettes, Dupuis-Williams and Baroud2011). Wu et al. (Reference Wu, Willing, Bjerketorp, Jansson and Hjort2009) have demonstrated kinematic separation of mixed bacteria streaming against a wall and shown that the larger bacteria have a faster rate than the smaller bacteria. However, there exist preferably a limited number of studies that have quantified the effects of convective inertia on the kinematics and energetics of swimming droplets (Li & Mao Reference Li and Mao2001; Mason & Moremedi Reference Mason and Moremedi2011) which are potential artificial analogues of biological systems.
Under the influence of inertial effects due to the external fluid, i.e. at finite Reynolds number (![]() $Re$), the leading-order approximation to the flow can be found by solving the standard Stokes equation. In an attempt to find the first-order correction due to the Reynolds number, an approximation via a regular perturbation expansion fails, as the computed velocity field invalidates the uniform far-field boundary condition and the higher approximations diverge at infinity. This is known as the Whitehead paradox in the literature (Whitehead Reference Whitehead1889). In the vicinity of the system, indicated as the Stokes or inner regime, the viscous effects are dominant. However, there exists an outer region as
$Re$), the leading-order approximation to the flow can be found by solving the standard Stokes equation. In an attempt to find the first-order correction due to the Reynolds number, an approximation via a regular perturbation expansion fails, as the computed velocity field invalidates the uniform far-field boundary condition and the higher approximations diverge at infinity. This is known as the Whitehead paradox in the literature (Whitehead Reference Whitehead1889). In the vicinity of the system, indicated as the Stokes or inner regime, the viscous effects are dominant. However, there exists an outer region as ![]() $r>O(Re^{-1})$, in which the strength of the inertial and viscous forces are comparable regardless of the low Reynolds number approximation. Subsequently, the Stokes solution is ineffectual. Oseen (Reference Oseen1910) fixed this paradox by identifying that the perturbation solution has a singularity at the far field and solved this by introducing a different length scale to rescale the governing equations. Proudman & Pearson (Reference Proudman and Pearson1957) were the first to utilize the approach of singular perturbation and the matched asymptotic expansion to solve the classical problem of low Reynolds number flow around a solid sphere and a circular cylinder. Later, in view of this, the inertial effect of a steady flow past a spherical liquid droplet with uniform interfacial tension was first considered by Taylor & Acrivos (Reference Taylor and Acrivos1964).
$r>O(Re^{-1})$, in which the strength of the inertial and viscous forces are comparable regardless of the low Reynolds number approximation. Subsequently, the Stokes solution is ineffectual. Oseen (Reference Oseen1910) fixed this paradox by identifying that the perturbation solution has a singularity at the far field and solved this by introducing a different length scale to rescale the governing equations. Proudman & Pearson (Reference Proudman and Pearson1957) were the first to utilize the approach of singular perturbation and the matched asymptotic expansion to solve the classical problem of low Reynolds number flow around a solid sphere and a circular cylinder. Later, in view of this, the inertial effect of a steady flow past a spherical liquid droplet with uniform interfacial tension was first considered by Taylor & Acrivos (Reference Taylor and Acrivos1964).
The velocity fields of a spherical droplet with a non-uniform interfacial tension up to first order in low Reynolds number flow was attempted by Mason & Moremedi (Reference Mason and Moremedi2011). Further, several studies have numerically investigated the Marangoni transport of droplets in presence of the convective effects of fluid inertia (Li & Mao Reference Li and Mao2001; Bäumler Reference Bäumler2014; Blyth & Pozrikidis Reference Blyth and Pozrikidis2014; Shardt, Masoud & Stone Reference Shardt, Masoud and Stone2016; Seric, Afkhami & Kondic Reference Seric, Afkhami and Kondic2018). Nevertheless, much less is known about how the inertial effect influences the swimming characteristics of a Marangoni droplet despite being relevant for artificial systems. A primary feature of self-induced Marangoni propulsion is to relate the prescribed surface activity to the migration velocity, which is useful for developing an artificial swimmer, and analyse how it is affected by the many factors of the surrounding medium, including the Reynolds number. Additionally, in the case of active suspensions, it is equally important to understand how the corresponding power dissipation and the swimming efficiency are controlled by the Reynolds number.
Following the classical solutions of Proudman & Pearson (Reference Proudman and Pearson1957) and Taylor & Acrivos (Reference Taylor and Acrivos1964) of improving the Stokes solution for a flow past a solid and a fluid sphere, respectively, in the present study we carefully utilize the matched asymptotic analysis of a spherical droplet driven by interfacial Marangoni flow at small, but non-zero Reynolds number and predict the effect of the convective inertia on the swimming velocity, power dissipation and swimming efficiency of the droplet swimmer. As mentioned earlier, the variation in the interfacial tension can arise due to different physical mechanisms. In the present work, we prescribe a generic description of the Marangoni effect across the surface of the spherical droplet independently of how the variability in the interfacial tension might have been induced. In this regard, we note that several other studies have examined the self-propulsion of solid bodies at small, but non-zero, Reynolds numbers, and have investigated the relevant swimming properties (Khair & Chisholm Reference Khair and Chisholm2011; Wang & Ardekani Reference Wang and Ardekani2011; Chisholm et al. Reference Chisholm, Legendre, Lauga and Khair2016). In this work, we probe the answers to similar questions for a Marangoni-driven axisymmetric droplet swimmer. Towards this, we explicitly calculate the interior and exterior streamfunctions and the associated swimming velocity up to the second order in Reynolds number and correlate the results to the swimming characteristics of a solid squirmer (Lighthill Reference Lighthill1952; Blake Reference Blake1971).
The paper is organized as follows. In § 2, we formulate the problem by introducing the governing equations and the related boundary conditions for Marangoni propulsion. In § 3, we employ the singular perturbation and the method of matched asymptotics to determine the analytical solution up to the first and second orders in Reynolds number. In §§ 4 and 5, we discuss the impact of the Reynolds number on the swimming characteristics of the droplet. We provide the main conclusions in § 6.
2. Mathematical model
We consider a spherical fluid droplet of radius ![]() $a$ and viscosity
$a$ and viscosity ![]() $\mu ^{i}$ which is moving with a velocity
$\mu ^{i}$ which is moving with a velocity ![]() $\boldsymbol {U}$ due to an inhomogeneous surface tension
$\boldsymbol {U}$ due to an inhomogeneous surface tension ![]() $\gamma$ at the interface in an unbounded stationary Newtonian fluid with a viscosity
$\gamma$ at the interface in an unbounded stationary Newtonian fluid with a viscosity ![]() $\mu ^{e}$. The fluids are of different viscosities and are assumed to be completely immiscible and incompressible. We assume that the resulting flow in the exterior domain (
$\mu ^{e}$. The fluids are of different viscosities and are assumed to be completely immiscible and incompressible. We assume that the resulting flow in the exterior domain (![]() $r>a$) due to the presence of the fluid droplet, is a steady low Reynolds number flow with velocity and pressure fields
$r>a$) due to the presence of the fluid droplet, is a steady low Reynolds number flow with velocity and pressure fields ![]() $(\boldsymbol {v}^{e},p^{e})$, while the velocity and pressure fields interior (
$(\boldsymbol {v}^{e},p^{e})$, while the velocity and pressure fields interior (![]() $r<a$) to the droplet
$r<a$) to the droplet ![]() $(\boldsymbol {v}^{i},p^{i})$ are assumed to be essentially viscous, i.e. at the zero Reynolds number regime. In view of these assumptions, the flow fields exterior as well as interior to the droplet satisfy the Navier–Stokes and Stokes equations, respectively, as (Kim & Karrila Reference Kim and Karrila2005)
$(\boldsymbol {v}^{i},p^{i})$ are assumed to be essentially viscous, i.e. at the zero Reynolds number regime. In view of these assumptions, the flow fields exterior as well as interior to the droplet satisfy the Navier–Stokes and Stokes equations, respectively, as (Kim & Karrila Reference Kim and Karrila2005)
where ![]() $Re= U a \rho ^e/\mu ^e <1$ is the Reynolds number associated with the exterior fluid with density
$Re= U a \rho ^e/\mu ^e <1$ is the Reynolds number associated with the exterior fluid with density ![]() $\rho ^e$. The above velocity and pressure fields are presented in a non-dimensionalized form via
$\rho ^e$. The above velocity and pressure fields are presented in a non-dimensionalized form via ![]() $\tilde {\boldsymbol {v}}^{e,i}=\boldsymbol {v}^{e,i}/\boldsymbol {U}$,
$\tilde {\boldsymbol {v}}^{e,i}=\boldsymbol {v}^{e,i}/\boldsymbol {U}$, ![]() $\tilde {r}=r/a$,
$\tilde {r}=r/a$, ![]() $\tilde {\boldsymbol {\nabla }}=a\,\boldsymbol {\nabla }$ and
$\tilde {\boldsymbol {\nabla }}=a\,\boldsymbol {\nabla }$ and ![]() $\tilde {p}^{e,i}= a\, p^{e,i}/\mu ^{e,i} |\boldsymbol {U}|$. We have further dropped the tilde notation for convenience. We now solve the problem within the reference frame moving with velocity
$\tilde {p}^{e,i}= a\, p^{e,i}/\mu ^{e,i} |\boldsymbol {U}|$. We have further dropped the tilde notation for convenience. We now solve the problem within the reference frame moving with velocity ![]() $\boldsymbol {U}$, which is the migration velocity of the droplet. Therefore, the exterior velocity field is expected to meet the migration velocity of the droplet in the limit
$\boldsymbol {U}$, which is the migration velocity of the droplet. Therefore, the exterior velocity field is expected to meet the migration velocity of the droplet in the limit ![]() $r\to \infty$. The inhomogeneous surface tension
$r\to \infty$. The inhomogeneous surface tension ![]() $(\gamma )$ across the interface is balanced by a stress jump at the fluid–fluid interface. Consequently, the boundary condition corresponding to the tangential stresses are formulated as (Saville Reference Saville1973; Levan Reference Levan1981)
$(\gamma )$ across the interface is balanced by a stress jump at the fluid–fluid interface. Consequently, the boundary condition corresponding to the tangential stresses are formulated as (Saville Reference Saville1973; Levan Reference Levan1981)
where ![]() $\boldsymbol {\varSigma }^e$,
$\boldsymbol {\varSigma }^e$, ![]() $\boldsymbol {\varSigma }^{i}$ are the stress tensors corresponding to the external and internal fluids;
$\boldsymbol {\varSigma }^{i}$ are the stress tensors corresponding to the external and internal fluids; ![]() $\boldsymbol {\hat {n}}$ and
$\boldsymbol {\hat {n}}$ and ![]() $\boldsymbol {\hat {t}}$ are the relevant normal and tangential unit vectors on the surface of the droplet. Further, we expand the inhomogeneous axisymmetric surface tension as
$\boldsymbol {\hat {t}}$ are the relevant normal and tangential unit vectors on the surface of the droplet. Further, we expand the inhomogeneous axisymmetric surface tension as ![]() $\gamma (\theta ) = \sum _{n=1}^{\infty } \gamma _n P_n(\cos \theta )$ with the strength
$\gamma (\theta ) = \sum _{n=1}^{\infty } \gamma _n P_n(\cos \theta )$ with the strength ![]() $\gamma _n$ and
$\gamma _n$ and ![]() $P_{n}(\cos \theta )$ are the Legendre polynomials. Now, (2.3) can be simplified in dimensionless form as
$P_{n}(\cos \theta )$ are the Legendre polynomials. Now, (2.3) can be simplified in dimensionless form as
where ![]() $\lambda =\mu ^{e}/\mu ^{i}$ is the viscosity ratio of the exterior fluid to the interior. The dimensionless stress field
$\lambda =\mu ^{e}/\mu ^{i}$ is the viscosity ratio of the exterior fluid to the interior. The dimensionless stress field ![]() $\boldsymbol {T_{s}}$ developed at the interface of the droplet given by
$\boldsymbol {T_{s}}$ developed at the interface of the droplet given by
 \begin{equation} \boldsymbol{T_{s}} = \sum_{n=1}^{\infty} \frac{2}{(n+1)} \frac{ \sigma_{n} \lambda}{U} \, \nabla_{s} P_{n}(\cos\theta), \end{equation}
\begin{equation} \boldsymbol{T_{s}} = \sum_{n=1}^{\infty} \frac{2}{(n+1)} \frac{ \sigma_{n} \lambda}{U} \, \nabla_{s} P_{n}(\cos\theta), \end{equation}
where ![]() $\sigma _{n}=(n+1) a^2 \gamma _n/ 2 \mu ^e$ denotes the corresponding strength. It is evident from the prescribed definition of
$\sigma _{n}=(n+1) a^2 \gamma _n/ 2 \mu ^e$ denotes the corresponding strength. It is evident from the prescribed definition of ![]() $\boldsymbol {T_s}$ that we have characterized the surface stress activity in an analogous mathematical structure to the slip velocity in the squirmer model (Lighthill Reference Lighthill1952; Blake Reference Blake1971) for further comparison to this classic model of an axisymmetric spherical micro-swimmer. The normal stress balance can be used to determine the shape change of the droplet, however, we restrict ourselves to the case of a spherical droplet. Although, Taylor & Acrivos (Reference Taylor and Acrivos1964) have shown that the deformation occurs for a spherical fluid droplet at first order in Reynolds number, however, in the case of Marangoni flows, the interfacial tension distribution allows the droplet to remain spherical as it induces an additional surface force across the interface (Stone & Leal Reference Stone and Leal1990; Hu & Lips Reference Hu and Lips2003). Furthermore, the surface of the droplet is impenetrable and the tangential fluxes are continuous across the fluid–fluid interface. Therefore, the associated conditions of immiscibility and continuity of the fluids lead to the following conditions for the normal and tangential velocity components, respectively,
$\boldsymbol {T_s}$ that we have characterized the surface stress activity in an analogous mathematical structure to the slip velocity in the squirmer model (Lighthill Reference Lighthill1952; Blake Reference Blake1971) for further comparison to this classic model of an axisymmetric spherical micro-swimmer. The normal stress balance can be used to determine the shape change of the droplet, however, we restrict ourselves to the case of a spherical droplet. Although, Taylor & Acrivos (Reference Taylor and Acrivos1964) have shown that the deformation occurs for a spherical fluid droplet at first order in Reynolds number, however, in the case of Marangoni flows, the interfacial tension distribution allows the droplet to remain spherical as it induces an additional surface force across the interface (Stone & Leal Reference Stone and Leal1990; Hu & Lips Reference Hu and Lips2003). Furthermore, the surface of the droplet is impenetrable and the tangential fluxes are continuous across the fluid–fluid interface. Therefore, the associated conditions of immiscibility and continuity of the fluids lead to the following conditions for the normal and tangential velocity components, respectively,
3. Analytical solution of the boundary value problem
In a simplified approach, we have regarded the migration of the droplet as an axisymmetric motion, and the associated streamfunctions ![]() $\psi ^{i,e}$ are utilized to describe the flow fields interior and exterior to the droplet, respectively (Happel & Brenner Reference Happel and Brenner1983). Correspondingly, the radial and the tangential components of velocity fields are expressed in terms of the streamfunction as
$\psi ^{i,e}$ are utilized to describe the flow fields interior and exterior to the droplet, respectively (Happel & Brenner Reference Happel and Brenner1983). Correspondingly, the radial and the tangential components of velocity fields are expressed in terms of the streamfunction as
where ![]() $\eta =\cos \theta$. The above streamfunctions are non-dimensionalized as
$\eta =\cos \theta$. The above streamfunctions are non-dimensionalized as ![]() $\psi ^{i,e}=\psi ^{i,e}/a^2 U$. Therefore, substituting (3.1a,b) in the momentum equations, (2.1) and (2.2) can be manifested as (Proudman & Pearson Reference Proudman and Pearson1957)
$\psi ^{i,e}=\psi ^{i,e}/a^2 U$. Therefore, substituting (3.1a,b) in the momentum equations, (2.1) and (2.2) can be manifested as (Proudman & Pearson Reference Proudman and Pearson1957)
where ![]() $E_{r}^{2}=\partial ^2/\partial r^2 + (1-\eta ^2)/r^2 \, \partial ^2/\partial \eta ^2$ and
$E_{r}^{2}=\partial ^2/\partial r^2 + (1-\eta ^2)/r^2 \, \partial ^2/\partial \eta ^2$ and ![]() $L_{r}=\eta /(1-\eta ^2) \, \partial /\partial r + 1/r \, \partial /\partial \eta$.Correspondingly, the far-field (
$L_{r}=\eta /(1-\eta ^2) \, \partial /\partial r + 1/r \, \partial /\partial \eta$.Correspondingly, the far-field (![]() $r\to \infty$) and the near-field (
$r\to \infty$) and the near-field (![]() $r=1$) boundary conditions can be expressed in terms of the streamfunction as
$r=1$) boundary conditions can be expressed in terms of the streamfunction as
and at ![]() $r=1$,
$r=1$,
In the induced stress field ![]() $\boldsymbol {T_s}$, we have asserted the first two terms (
$\boldsymbol {T_s}$, we have asserted the first two terms (![]() $n=2$) of the general series (see (2.5)) to proceed with the calculation. Accordingly, we have defined
$n=2$) of the general series (see (2.5)) to proceed with the calculation. Accordingly, we have defined ![]() $\sigma =\sigma _2/\sigma _1$ as the relative strength of the first two modes. The flow around the droplet is analysed for small Reynolds number
$\sigma =\sigma _2/\sigma _1$ as the relative strength of the first two modes. The flow around the droplet is analysed for small Reynolds number ![]() $Re$; thus, it is required that we must have
$Re$; thus, it is required that we must have ![]() $\sigma Re < 1$ in addition to the condition
$\sigma Re < 1$ in addition to the condition ![]() $Re < 1$.
$Re < 1$.
3.1. Singular perturbation technique
It may be noted that the available Stokes solution of the Marangoni propulsion of a fluid droplet does not provide a valid correction when the viscous and inertial effects are comparable (Whitehead Reference Whitehead1889). The solution breaks down in the limit ![]() $r \geq O(Re^{-1})$ under the aforementioned boundary conditions. In this context, the problem of low Reynolds number flow around the Marangoni droplet may be considered as a singular perturbation problem (Van Dyke Reference Van Dyke1975; Hsiao & MacCamy Reference Hsiao and MacCamy1982). Consequently, we adopt the singular perturbation technique followed by the method of matched asymptotic (Kaplun Reference Kaplun1957; Proudman & Pearson Reference Proudman and Pearson1957) to analytically obtain the asymptotic expansions of the governing streamfunctions of the interior and exterior fluids and analyse the kinematics and energetics of a Marangoni-driven droplet (figure 1).
$r \geq O(Re^{-1})$ under the aforementioned boundary conditions. In this context, the problem of low Reynolds number flow around the Marangoni droplet may be considered as a singular perturbation problem (Van Dyke Reference Van Dyke1975; Hsiao & MacCamy Reference Hsiao and MacCamy1982). Consequently, we adopt the singular perturbation technique followed by the method of matched asymptotic (Kaplun Reference Kaplun1957; Proudman & Pearson Reference Proudman and Pearson1957) to analytically obtain the asymptotic expansions of the governing streamfunctions of the interior and exterior fluids and analyse the kinematics and energetics of a Marangoni-driven droplet (figure 1).
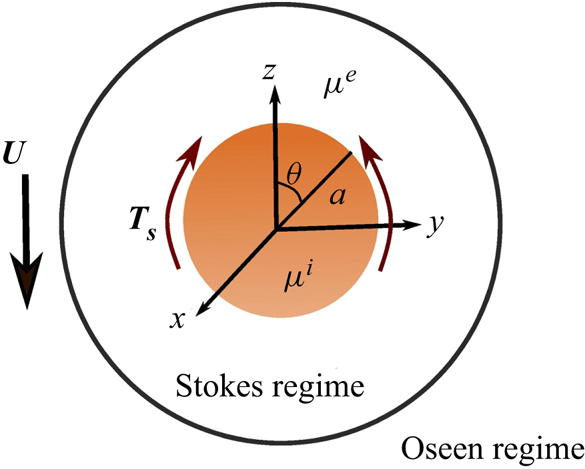
Figure 1. The schematic representation of the droplet (of viscosity ![]() $\mu ^i$) with an interfacial stress field
$\mu ^i$) with an interfacial stress field ![]() $\boldsymbol {T_s}$ in a low Reynolds number fluid of viscosity
$\boldsymbol {T_s}$ in a low Reynolds number fluid of viscosity ![]() $\mu ^e$ (
$\mu ^e$ (![]() $<\mu ^i$). A fictitious boundary separates the Stokes and Oseen regimes;
$<\mu ^i$). A fictitious boundary separates the Stokes and Oseen regimes; ![]() $\boldsymbol {U}$ indicates the far-field migration velocity of the droplet in the Oseen regime.
$\boldsymbol {U}$ indicates the far-field migration velocity of the droplet in the Oseen regime.
3.1.1. Inner or Stokes regime
In the matched asymptotic expansions, we decompose the continuous phase of the fluid (![]() $r>1$) into two separate overlapping regions, the Stokes or the inner regime and the Oseen or outer regime. In the Stokes regime, where
$r>1$) into two separate overlapping regions, the Stokes or the inner regime and the Oseen or outer regime. In the Stokes regime, where ![]() $r\sim O(1)$ and
$r\sim O(1)$ and ![]() $Re < 1$, we consider that the viscous effects are dominant and the exterior streamfunction is manifested as
$Re < 1$, we consider that the viscous effects are dominant and the exterior streamfunction is manifested as
such that ![]() $f_{n+1}(Re)/f_{n}(Re) \to 0 \ \text {as}\ Re\to 0$. Also, we have assumed that the fluid interior (
$f_{n+1}(Re)/f_{n}(Re) \to 0 \ \text {as}\ Re\to 0$. Also, we have assumed that the fluid interior (![]() $r<1$) to the droplet is highly viscous and obeys the Stokes equation. Consequently, we adopt a similar expansion for the interior streamfunction
$r<1$) to the droplet is highly viscous and obeys the Stokes equation. Consequently, we adopt a similar expansion for the interior streamfunction ![]() $\psi ^{i}$ as
$\psi ^{i}$ as
where we have used the same expansion coefficients that were used in the exterior streamfunction for simplifying the calculations. The inner expansion of the streamfunctions ![]() $\psi ^{e}$ and
$\psi ^{e}$ and ![]() $\psi ^{i}$, i.e. (3.8) and (3.9), must satisfy the equations (3.2) and (3.3), respectively, along with the boundary conditions (3.5)–(3.7). The inner expressions are valid in the Stokes regime, therefore, we are restricted to adopt the far-field condition (as in (3.4)) directly. However, the contribution of the far field in the inner expansions of the exterior and interior streamfunctions (
$\psi ^{i}$, i.e. (3.8) and (3.9), must satisfy the equations (3.2) and (3.3), respectively, along with the boundary conditions (3.5)–(3.7). The inner expressions are valid in the Stokes regime, therefore, we are restricted to adopt the far-field condition (as in (3.4)) directly. However, the contribution of the far field in the inner expansions of the exterior and interior streamfunctions (![]() $\psi ^{e}$ or
$\psi ^{e}$ or ![]() $\psi ^{i}$) are later obtained through the matching condition with the outer expansion corresponding to the Oseen region (Proudman & Pearson Reference Proudman and Pearson1957).
$\psi ^{i}$) are later obtained through the matching condition with the outer expansion corresponding to the Oseen region (Proudman & Pearson Reference Proudman and Pearson1957).
3.1.2. Outer or Oseen regime
In the outer (Oseen) region, where ![]() $r \sim O(Re^{-1})$, the inertial term
$r \sim O(Re^{-1})$, the inertial term ![]() $Re (\boldsymbol {v^e} \boldsymbol {\cdot } \boldsymbol {\nabla }) \boldsymbol {\cdot } \boldsymbol {v^e}$ from the Navier–Stokes equation ((2.1)) is not negligible and, hence, in this region the inner expansion of the exterior streamfunction ((3.8)) is not valid. This can be avoided by using a suitable length scale to rescale the equation (Oseen Reference Oseen1910). Accordingly, the Oseen variables are defined as
$Re (\boldsymbol {v^e} \boldsymbol {\cdot } \boldsymbol {\nabla }) \boldsymbol {\cdot } \boldsymbol {v^e}$ from the Navier–Stokes equation ((2.1)) is not negligible and, hence, in this region the inner expansion of the exterior streamfunction ((3.8)) is not valid. This can be avoided by using a suitable length scale to rescale the equation (Oseen Reference Oseen1910). Accordingly, the Oseen variables are defined as
and a straightforward substitution will ascertain (3.2) that
where the operators ![]() $E_{\hat {r}}^{2}$ and
$E_{\hat {r}}^{2}$ and ![]() $L_{\hat {r}}$ are similar to those defined in the former section. The corresponding far-field condition ((3.4)) takes the form
$L_{\hat {r}}$ are similar to those defined in the former section. The corresponding far-field condition ((3.4)) takes the form
As before, the exterior streamfunction in the Oseen region is expressed as
where ![]() $F_{n+1}(Re)/F_{n}(Re) \to 0 \ \text {as}\ Re \to 0.$
$F_{n+1}(Re)/F_{n}(Re) \to 0 \ \text {as}\ Re \to 0.$
3.2. Leading-order calculation
The leading-order solution of the Stokes expansion of the interior streamfunction (![]() $r<1$) satisfies the Stokes equation
$r<1$) satisfies the Stokes equation ![]() $E_{r}^{4}\psi _{0}^{i}=0$. Therefore, an appropriate solution which is regular at the origin (
$E_{r}^{4}\psi _{0}^{i}=0$. Therefore, an appropriate solution which is regular at the origin (![]() $r\to 0$) is given by Happel & Brenner (Reference Happel and Brenner1983)
$r\to 0$) is given by Happel & Brenner (Reference Happel and Brenner1983)
 \begin{equation} \psi_0^{i}=\sum_{n=1}^{\infty} \left( C_{n}^{i} r^{n+1} + D_{n}^{i} r^{n+3} \right) Q_{n}(\eta), \end{equation}
\begin{equation} \psi_0^{i}=\sum_{n=1}^{\infty} \left( C_{n}^{i} r^{n+1} + D_{n}^{i} r^{n+3} \right) Q_{n}(\eta), \end{equation}
where ![]() $C_{n}^{i}$ and
$C_{n}^{i}$ and ![]() $D_{n}^{i}$ are the unknown coefficients, and
$D_{n}^{i}$ are the unknown coefficients, and ![]() $Q_{n}(\eta )= \int _{-1}^{\eta } P_n(\eta ^{\prime }) d\eta ^{\prime }$. Likewise, the leading order of the Stokes expansion of the exterior streamfunction (3.8) also satisfies
$Q_{n}(\eta )= \int _{-1}^{\eta } P_n(\eta ^{\prime }) d\eta ^{\prime }$. Likewise, the leading order of the Stokes expansion of the exterior streamfunction (3.8) also satisfies ![]() $E_{r}^{4}\psi _{0}^{e}=0$, thus, the solution can be computed as
$E_{r}^{4}\psi _{0}^{e}=0$, thus, the solution can be computed as
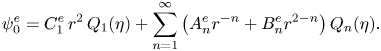 \begin{equation} \psi_{0}^{e}= C_1^e\, r^2\, Q_1(\eta) + \sum_{n=1}^{\infty} \left (A^{e}_{n} r^{-n} + B^{e}_{n} r^{2-n}\right) Q_{n}(\eta). \end{equation}
\begin{equation} \psi_{0}^{e}= C_1^e\, r^2\, Q_1(\eta) + \sum_{n=1}^{\infty} \left (A^{e}_{n} r^{-n} + B^{e}_{n} r^{2-n}\right) Q_{n}(\eta). \end{equation}
It may be noted that the above solution of the exterior streamfunction is obtained by avoiding the singularities and in view of the uniform far-field streamfunction in the limit ![]() $r\to \infty$. It is evident that, concerning the uniform far field and the prescribed surface activity ((3.7)), the higher-order (
$r\to \infty$. It is evident that, concerning the uniform far field and the prescribed surface activity ((3.7)), the higher-order (![]() $n\geq 3$) terms in the general expansions of the interior and exterior streamfunctions are zero. Correspondingly, the unknown coefficients
$n\geq 3$) terms in the general expansions of the interior and exterior streamfunctions are zero. Correspondingly, the unknown coefficients ![]() $(C^{i}_n, D^{i}_n)$ and
$(C^{i}_n, D^{i}_n)$ and ![]() $(A^{e}_{n}, B^{e}_{n})$ can be determined by employing the aforesaid boundary conditions at the fluid–fluid interface. However, the coefficient of far field, i.e.
$(A^{e}_{n}, B^{e}_{n})$ can be determined by employing the aforesaid boundary conditions at the fluid–fluid interface. However, the coefficient of far field, i.e. ![]() $C^{e}_1$, can be determined by matching the leading-order solutions of the Stokes and Oseen regimes. Thus, the general solutions of the leading-order interior (
$C^{e}_1$, can be determined by matching the leading-order solutions of the Stokes and Oseen regimes. Thus, the general solutions of the leading-order interior (![]() $r<1$) and exterior (
$r<1$) and exterior (![]() $r>1$) streamfunctions can be obtained as
$r>1$) streamfunctions can be obtained as
 \begin{align} \psi_{0}^{e} & = \left( C_{1}^{e} r^2 - \frac{((3 +2 \lambda) C_{1}^{e} - 2 \sigma_1 \lambda/3 U)}{2 (1+\lambda)} \, r + \frac{(C_{1}^{e} - 2 \sigma_1 \lambda/3 U)}{2 (1+\lambda) r} \right) Q_{1}(\eta) \nonumber\\ &\quad + \frac{2 \sigma_2 \lambda}{(5 U (1+\lambda))} \left( 1 - \frac{1}{r^2} \right)\, Q_{2}(\eta). \end{align}
\begin{align} \psi_{0}^{e} & = \left( C_{1}^{e} r^2 - \frac{((3 +2 \lambda) C_{1}^{e} - 2 \sigma_1 \lambda/3 U)}{2 (1+\lambda)} \, r + \frac{(C_{1}^{e} - 2 \sigma_1 \lambda/3 U)}{2 (1+\lambda) r} \right) Q_{1}(\eta) \nonumber\\ &\quad + \frac{2 \sigma_2 \lambda}{(5 U (1+\lambda))} \left( 1 - \frac{1}{r^2} \right)\, Q_{2}(\eta). \end{align}
Now, the leading-order solution in the Oseen regime should necessarily agree with the uniform far-field condition at infinity. Consequently, we indicate ![]() $\varPsi _{0}^{e}$ as (from (3.12))
$\varPsi _{0}^{e}$ as (from (3.12))
3.2.1. Determination of  $C_1^e$
$C_1^e$
In order to match the leading-order solutions of the Stokes and Oseen regimes, we further express (3.17) in terms of the Oseen variables and consider the limit ![]() $Re \to 0$. This would imply that
$Re \to 0$. This would imply that ![]() $C_{1}^{e}=-1$. Thus, Stokes solution for the Marangoni-driven droplet is recovered (Balasubramaniam & Subramanian Reference Balasubramaniam and Subramanian2000; Schmitt & Stark Reference Schmitt and Stark2016b).
$C_{1}^{e}=-1$. Thus, Stokes solution for the Marangoni-driven droplet is recovered (Balasubramaniam & Subramanian Reference Balasubramaniam and Subramanian2000; Schmitt & Stark Reference Schmitt and Stark2016b).
3.3. First-order corrections
Under the assumption of negligible inertial effect, the first order of the interior streamfunction gives rise to the Stokes equation, i.e. ![]() $E_{r}^{4}\psi _{1}^{i}=0$, which admits a general solution as been mentioned in (3.14). On the other hand, after substituting (3.8) and (3.13) in (3.2) and (3.11), respectively, the governing equations for the first-order exterior streamfunction in the Stokes and Oseen regimes, respectively, can be obtained as
$E_{r}^{4}\psi _{1}^{i}=0$, which admits a general solution as been mentioned in (3.14). On the other hand, after substituting (3.8) and (3.13) in (3.2) and (3.11), respectively, the governing equations for the first-order exterior streamfunction in the Stokes and Oseen regimes, respectively, can be obtained as
In the following, we set ![]() $f_{1}(Re) = Re$ without the loss of generality (Proudman & Pearson Reference Proudman and Pearson1957). Further, by substituting (3.17) in (3.19), the governing equation of
$f_{1}(Re) = Re$ without the loss of generality (Proudman & Pearson Reference Proudman and Pearson1957). Further, by substituting (3.17) in (3.19), the governing equation of ![]() $\psi _{1}^{e}$ can be simplified to,
$\psi _{1}^{e}$ can be simplified to,
 \begin{align} E_{r}^{4}\psi_{1}^{e} & = \left( \frac{6\, A_2^e B_1^e}{5 r^4} + \frac{6\, A_2^e}{5 r^6} \left( B_1^e + 6 A_1^e \right) \right)\, Q_1(\eta) \nonumber\\ &\quad + \left( \frac{6\, B_1^e}{r^2} - \frac{6\, (B_1^e)^2}{r^3} - \frac{6\, A_1^e B_1^e}{r^5} -\frac{24 (A_2^e)^2}{7 r^5} + \frac{48\, (A_2^e)^2}{7 r^4} \right)\, Q_2(\eta) \nonumber\\ &\quad + \left( \frac{144\, A_2^e B_1^e}{5 r^4} - \frac{24\, A_2^e}{r^3} + \frac{84\, A_2^e A_1^e}{5 r^6} - \frac{36\, A_2^e B_1^e}{5 r^6} \right)\, Q_3(\eta) \nonumber\\ &\quad + \left( \frac{120\, (A_2^e)^2}{7 r^7} -\frac{ 144\, (A_2^e)^2}{7 r^7} \right)\, Q_4(\eta), \end{align}
\begin{align} E_{r}^{4}\psi_{1}^{e} & = \left( \frac{6\, A_2^e B_1^e}{5 r^4} + \frac{6\, A_2^e}{5 r^6} \left( B_1^e + 6 A_1^e \right) \right)\, Q_1(\eta) \nonumber\\ &\quad + \left( \frac{6\, B_1^e}{r^2} - \frac{6\, (B_1^e)^2}{r^3} - \frac{6\, A_1^e B_1^e}{r^5} -\frac{24 (A_2^e)^2}{7 r^5} + \frac{48\, (A_2^e)^2}{7 r^4} \right)\, Q_2(\eta) \nonumber\\ &\quad + \left( \frac{144\, A_2^e B_1^e}{5 r^4} - \frac{24\, A_2^e}{r^3} + \frac{84\, A_2^e A_1^e}{5 r^6} - \frac{36\, A_2^e B_1^e}{5 r^6} \right)\, Q_3(\eta) \nonumber\\ &\quad + \left( \frac{120\, (A_2^e)^2}{7 r^7} -\frac{ 144\, (A_2^e)^2}{7 r^7} \right)\, Q_4(\eta), \end{align}
where ![]() $A_1^e, B_1^e, A_2^e$ are the coefficients of the leading-order solution of the exterior streamfunction in the Stokes regime (see (3.15)) which have been determined using the boundary conditions mentioned in § 3.2. It may be noted that without explicit substitution of the coefficients, the structure of inhomogeneous part of (3.21) appears identical to the analysis by Wang & Ardekani (Reference Wang and Ardekani2011) for the inertial effects on a squirmer. Accordingly, we write the general solution of (3.21) as
$A_1^e, B_1^e, A_2^e$ are the coefficients of the leading-order solution of the exterior streamfunction in the Stokes regime (see (3.15)) which have been determined using the boundary conditions mentioned in § 3.2. It may be noted that without explicit substitution of the coefficients, the structure of inhomogeneous part of (3.21) appears identical to the analysis by Wang & Ardekani (Reference Wang and Ardekani2011) for the inertial effects on a squirmer. Accordingly, we write the general solution of (3.21) as ![]() $\psi _{1}^e=\sum _{n=1}^{4} g_{n}(r)\, Q_n(\eta )$, where
$\psi _{1}^e=\sum _{n=1}^{4} g_{n}(r)\, Q_n(\eta )$, where
 \begin{equation} \left. \begin{array}{c@{}}
\displaystyle g_1(r) = \left(\frac{\alpha_1^e}{r} + \beta_1^e r +
\gamma_1^e r^2 - \frac{3}{20} A_2^e B_1^e + \frac{A_2^e}{10
r^2} \left(A_1^e + B_1^e/6 \right) \right),\\
\displaystyle g_2(r) =
\left( \frac{\alpha_2^e}{r^{2}} + \beta_2^e -
\frac{(B_1^e)^2}{4} r + \frac{B_1^e}{4} r^2 +
\left(\frac{A_1^e B_1^e}{4} + \frac{(A_2^e)^2}{7}
\right)\,\frac{1}{r} + \frac{(A_2^e)^2}{21 r^3} \right), \\
\displaystyle g_3(r) = \left( \frac{\alpha_3^e}{r^{3}} +
\frac{\beta_3^e}{r^{1}} + \frac{2}{5} A_2^e B_1^e -
\frac{A_2^e}{5} r + \frac{1}{20 r^2} \left(-7 A_2^e A_1^e +
3 A_2^e B_1^e \right) \right),\\
\displaystyle g_4(r) = \left(
\frac{\alpha_4^e}{r^{4}} + \frac{\beta_4^e}{r^{2}}
-\frac{(A_2^e)^2}{7 r} -\frac{3 (A_{2}^e)^2}{14 r^3}
\right). \end{array} \right\}
\end{equation}
\begin{equation} \left. \begin{array}{c@{}}
\displaystyle g_1(r) = \left(\frac{\alpha_1^e}{r} + \beta_1^e r +
\gamma_1^e r^2 - \frac{3}{20} A_2^e B_1^e + \frac{A_2^e}{10
r^2} \left(A_1^e + B_1^e/6 \right) \right),\\
\displaystyle g_2(r) =
\left( \frac{\alpha_2^e}{r^{2}} + \beta_2^e -
\frac{(B_1^e)^2}{4} r + \frac{B_1^e}{4} r^2 +
\left(\frac{A_1^e B_1^e}{4} + \frac{(A_2^e)^2}{7}
\right)\,\frac{1}{r} + \frac{(A_2^e)^2}{21 r^3} \right), \\
\displaystyle g_3(r) = \left( \frac{\alpha_3^e}{r^{3}} +
\frac{\beta_3^e}{r^{1}} + \frac{2}{5} A_2^e B_1^e -
\frac{A_2^e}{5} r + \frac{1}{20 r^2} \left(-7 A_2^e A_1^e +
3 A_2^e B_1^e \right) \right),\\
\displaystyle g_4(r) = \left(
\frac{\alpha_4^e}{r^{4}} + \frac{\beta_4^e}{r^{2}}
-\frac{(A_2^e)^2}{7 r} -\frac{3 (A_{2}^e)^2}{14 r^3}
\right). \end{array} \right\}
\end{equation}
The above expressions are determined considering the fact that the streamfunction in the Stokes regime should not contain higher-order terms (in ![]() $r$) than the uniform far-field streamfunction. All the unknown coefficients (
$r$) than the uniform far-field streamfunction. All the unknown coefficients (![]() $\alpha _n^e,\beta _n^e$) and (
$\alpha _n^e,\beta _n^e$) and (![]() $C_n^i, D_n^i$) at
$C_n^i, D_n^i$) at ![]() $O(Re)$ are to be determined from the boundary conditions mentioned in (3.5)–(3.7). Further, to determine
$O(Re)$ are to be determined from the boundary conditions mentioned in (3.5)–(3.7). Further, to determine ![]() $\gamma _1^e$, we match the coefficient of the highest order of
$\gamma _1^e$, we match the coefficient of the highest order of ![]() $r$ in
$r$ in ![]() $\psi _1^e$ (i.e.
$\psi _1^e$ (i.e. ![]() $r^2$) to the same in the first-order solution in the Oseen regime, which we determine in what follows.
$r^2$) to the same in the first-order solution in the Oseen regime, which we determine in what follows.
According to Goldstein (Reference Goldstein1929), (3.20) can be solved using a transformation ![]() $E_{\hat {r}}^{2}\varPsi _{1}^{e}= \textrm {e}^{\hat {r}\eta /2}\phi$. Hence, the general solution of
$E_{\hat {r}}^{2}\varPsi _{1}^{e}= \textrm {e}^{\hat {r}\eta /2}\phi$. Hence, the general solution of ![]() $\varPsi ^e_1$ that vanishes at infinity and
$\varPsi ^e_1$ that vanishes at infinity and ![]() $\eta ={\pm }1$ can be determined as (Proudman & Pearson Reference Proudman and Pearson1957) (for details see appendix A)
$\eta ={\pm }1$ can be determined as (Proudman & Pearson Reference Proudman and Pearson1957) (for details see appendix A)
3.3.1. Determination of  $\gamma _1^{e}$
$\gamma _1^{e}$
From the first-order solutions in the Stokes regime (i.e. ![]() $\psi _{1}^{e}$) and Oseen regime (i.e.
$\psi _{1}^{e}$) and Oseen regime (i.e. ![]() $\varPsi _{1}^{e}$), the coefficient of the highest-order term
$\varPsi _{1}^{e}$), the coefficient of the highest-order term ![]() $r^2$ or
$r^2$ or ![]() $\hat {r}^2$ can be identified as
$\hat {r}^2$ can be identified as
In view of the matching condition, (3.25) can be expressed in term of the Oseen variables. Correspondingly, (3.24) should agree with (3.25), and ![]() $\gamma _1^{e}$ which determines
$\gamma _1^{e}$ which determines ![]() $\gamma _1^e = -B_1^e/4$. This is supported by the results of Wang & Ardekani (Reference Wang and Ardekani2011).
$\gamma _1^e = -B_1^e/4$. This is supported by the results of Wang & Ardekani (Reference Wang and Ardekani2011).
3.4. Second-order correction
From (3.2) and (3.11), the governing equations for the second-order exterior streamfunction in the inner and Oseen regimes are respectively given by
where we have set ![]() $f_2(Re)=Re^2$ in the inner regime without loss of generality. Further, using the solutions for
$f_2(Re)=Re^2$ in the inner regime without loss of generality. Further, using the solutions for ![]() $\psi _0^e$ and
$\psi _0^e$ and ![]() $\psi _1^e$ ((3.17) and (3.22)), the inhomogeneous part (right-hand side) of (3.26) can be obtained in accordance with the angular dependency
$\psi _1^e$ ((3.17) and (3.22)), the inhomogeneous part (right-hand side) of (3.26) can be obtained in accordance with the angular dependency ![]() $Q_{n}(\eta )$. It may be noted that, due to the arduous structure of the inhomogeneous part, we pursue the solution of the second-order streamfunction
$Q_{n}(\eta )$. It may be noted that, due to the arduous structure of the inhomogeneous part, we pursue the solution of the second-order streamfunction ![]() $\psi _2^e$ up to the first mode (
$\psi _2^e$ up to the first mode (![]() $n=1$), i.e. the contribution of the streamfunction that is necessary for determining the migration velocity. A straightforward calculation of the complementary solution and the particular integral yields
$n=1$), i.e. the contribution of the streamfunction that is necessary for determining the migration velocity. A straightforward calculation of the complementary solution and the particular integral yields
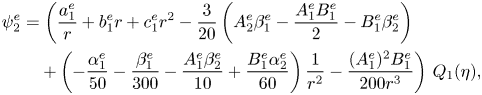 \begin{align} \psi_2^e & = \left( \frac{a_1^e}{r} + b_1^e r + c_1^e r^2 - \frac{3}{20} \left( A_2^e \beta_1^e - \frac{A_1^e B_1^e}{2} - B_1^e \beta_2^e \right) \right. \nonumber\\ &\quad \left. + \left( -\frac{\alpha_1^e}{50} - \frac{\beta_1^e}{300} - \frac{A_1^e \beta_2^e}{10} + \frac{B_1^e \alpha_2^e}{60} \right)\frac{1}{r^2} - \frac{(A_1^e)^2 B_1^e}{200 r^3} \right)\, Q_1(\eta), \end{align}
\begin{align} \psi_2^e & = \left( \frac{a_1^e}{r} + b_1^e r + c_1^e r^2 - \frac{3}{20} \left( A_2^e \beta_1^e - \frac{A_1^e B_1^e}{2} - B_1^e \beta_2^e \right) \right. \nonumber\\ &\quad \left. + \left( -\frac{\alpha_1^e}{50} - \frac{\beta_1^e}{300} - \frac{A_1^e \beta_2^e}{10} + \frac{B_1^e \alpha_2^e}{60} \right)\frac{1}{r^2} - \frac{(A_1^e)^2 B_1^e}{200 r^3} \right)\, Q_1(\eta), \end{align}
where the unknown coefficients ![]() $a_1^e$ and
$a_1^e$ and ![]() $b_1^e$ can be determined from the boundary conditions prescribed in (3.5)–(3.7) and the coefficient
$b_1^e$ can be determined from the boundary conditions prescribed in (3.5)–(3.7) and the coefficient ![]() $c_1^e$ from the matching condition with the second-order streamfunction in the Oseen regime.
$c_1^e$ from the matching condition with the second-order streamfunction in the Oseen regime.
Regarding this, we notice that the governing equation for ![]() $\varPsi _2^e$ in the Oseen regime is identical to (3.20) with
$\varPsi _2^e$ in the Oseen regime is identical to (3.20) with ![]() $\varPsi _1^e$ replaced by
$\varPsi _1^e$ replaced by ![]() $\varPsi _2^e$. Therefore, a solution up to the first mode (
$\varPsi _2^e$. Therefore, a solution up to the first mode (![]() $Q_1(\eta )$) is analogous to (A 1). Additionally, the first mode contribution of the derived inner streamfunction ( i.e.
$Q_1(\eta )$) is analogous to (A 1). Additionally, the first mode contribution of the derived inner streamfunction ( i.e. ![]() $\psi ^e \sim \psi _0^e + Re \, \psi _1^e$) in the Oseen regime is quantified as
$\psi ^e \sim \psi _0^e + Re \, \psi _1^e$) in the Oseen regime is quantified as ![]() $E^2 \psi ^e \sim - 2 \beta _1^e Q_1(\eta )/r$ at
$E^2 \psi ^e \sim - 2 \beta _1^e Q_1(\eta )/r$ at ![]() $O(Re^2)$. Consequently, the unknown coefficient
$O(Re^2)$. Consequently, the unknown coefficient ![]() $\mathcal {A}_1$ for the second-order streamfunction in the Oseen regime is retrieved as
$\mathcal {A}_1$ for the second-order streamfunction in the Oseen regime is retrieved as ![]() $\mathcal {A}_1= -\beta _1^e$. Furthermore, an appropriate matching condition yields
$\mathcal {A}_1= -\beta _1^e$. Furthermore, an appropriate matching condition yields ![]() $c_1^e=-\beta _1^e/4$.
$c_1^e=-\beta _1^e/4$.
In this context, the fundamental difference between a passive and an active spherical body was noted by Khair & Chisholm (Reference Khair and Chisholm2011). For any creeping flow past a passive droplet, due to the existence of a uniform far-field velocity of the ambient medium, a finite net force acts on the surface of the body, whereas, for an active self-propelling system, due to the force-free nature of the motion, the far-field velocity typically indicates the migration velocity of the swimmer. Apparently, by virtue of this, the logarithm terms (![]() $O(Re^2 \ln Re)$), which appear in the second order in the Stokes expansion for a passive system, do not appear at
$O(Re^2 \ln Re)$), which appear in the second order in the Stokes expansion for a passive system, do not appear at ![]() $O(Re^2)$ (Khair & Chisholm Reference Khair and Chisholm2011) for active systems. This summarizes the complete calculation of the streamfunctions in the Stokes and Oseen regimes for a Marangoni-driven droplet up to
$O(Re^2)$ (Khair & Chisholm Reference Khair and Chisholm2011) for active systems. This summarizes the complete calculation of the streamfunctions in the Stokes and Oseen regimes for a Marangoni-driven droplet up to ![]() $O(Re)$ and an approximated first mode solution for the exterior streamfunction at
$O(Re)$ and an approximated first mode solution for the exterior streamfunction at ![]() $O(Re^2)$. In the following sections, we allude the significance of this inertial forcing encountered by the droplet on its swimming motility, flow fields and energy expenditures utilizing the complete general solutions up to
$O(Re^2)$. In the following sections, we allude the significance of this inertial forcing encountered by the droplet on its swimming motility, flow fields and energy expenditures utilizing the complete general solutions up to ![]() $O(Re)$ and comment on the distinctness of the first-order and second-order corrected migration velocities.
$O(Re)$ and comment on the distinctness of the first-order and second-order corrected migration velocities.
4. Results: first-order correction
4.1. Drag on the surface of the droplet
For evaluation of the drag on the surface of the droplet, we proceed with the streamfunction (![]() $\psi ^{e}= \psi _{0}^{e} + Re\, \psi _{1}^{e}$) in the Stokes or inner regime which is well founded in the vicinity of the droplet. For axisymmetric swimming, the non-zero component of the drag force acting in the
$\psi ^{e}= \psi _{0}^{e} + Re\, \psi _{1}^{e}$) in the Stokes or inner regime which is well founded in the vicinity of the droplet. For axisymmetric swimming, the non-zero component of the drag force acting in the ![]() $z$-direction is given by
$z$-direction is given by
where ![]() $\textrm {d}s$ is the surface element of the droplet. Having computed the velocity fields from the streamfunction, we further obtain the corresponding stresses and arrive at the following expression for dimensionless drag force
$\textrm {d}s$ is the surface element of the droplet. Having computed the velocity fields from the streamfunction, we further obtain the corresponding stresses and arrive at the following expression for dimensionless drag force
where ![]() $D_0$ and
$D_0$ and ![]() $D_1$ are evaluated as
$D_1$ are evaluated as
with ![]() $U \to U/U_0$ as the dimensionless velocity of the droplet. We have used
$U \to U/U_0$ as the dimensionless velocity of the droplet. We have used ![]() $U_0 = -2\sigma _1\lambda /(3 (3+2\lambda ))$ as the reference scale, which is the standard locomotion speed for a Marangoni stress-driven droplet in the limit
$U_0 = -2\sigma _1\lambda /(3 (3+2\lambda ))$ as the reference scale, which is the standard locomotion speed for a Marangoni stress-driven droplet in the limit ![]() $Re \to 0$ (Schmitt & Stark Reference Schmitt and Stark2016b). For self-propulsion of the droplet, the net drag (
$Re \to 0$ (Schmitt & Stark Reference Schmitt and Stark2016b). For self-propulsion of the droplet, the net drag (![]() $D$) must vanish on the surface of the droplet. Consequently, we arrive at the following quadratic equation in
$D$) must vanish on the surface of the droplet. Consequently, we arrive at the following quadratic equation in ![]() $U$,
$U$,
 \begin{align} D & = \left( 2 + Re\, \frac{3+2\lambda}{4 (1+\lambda)} \right)\,\, U^2 - \left( 2 + Re\, \frac{11 +10 \lambda }{4 (1+\lambda)} + Re\, \sigma\, \frac{ (36 + 67 \lambda + 26 \lambda^2) }{ 250 (1+\lambda)^2} \right) \, U \nonumber\\ &\quad - Re \, \sigma\, \frac{ (2+\lambda) (3+2\lambda) }{50 (1+\lambda)^2} =0. \end{align}
\begin{align} D & = \left( 2 + Re\, \frac{3+2\lambda}{4 (1+\lambda)} \right)\,\, U^2 - \left( 2 + Re\, \frac{11 +10 \lambda }{4 (1+\lambda)} + Re\, \sigma\, \frac{ (36 + 67 \lambda + 26 \lambda^2) }{ 250 (1+\lambda)^2} \right) \, U \nonumber\\ &\quad - Re \, \sigma\, \frac{ (2+\lambda) (3+2\lambda) }{50 (1+\lambda)^2} =0. \end{align}
The migration velocity ![]() $U$ can be determined by solving the above quadratic equation up to
$U$ can be determined by solving the above quadratic equation up to ![]() $O(Re)$ limit. The approximated solutions can be written as
$O(Re)$ limit. The approximated solutions can be written as
It may be noted that the above solutions are obtained subject to the constraint ![]() $\lambda <1$ up to
$\lambda <1$ up to ![]() $O(\lambda ^2)$. This constraint indicates that the interior fluid is more viscous than the exterior, consistent with our prior assumption. Correspondingly, the
$O(\lambda ^2)$. This constraint indicates that the interior fluid is more viscous than the exterior, consistent with our prior assumption. Correspondingly, the ![]() $\sigma Re \lambda <1$ and
$\sigma Re \lambda <1$ and ![]() $\sigma Re \lambda ^2 <1$ conditions are maintained in the further calculations. We observe that
$\sigma Re \lambda ^2 <1$ conditions are maintained in the further calculations. We observe that ![]() $U_1^*$ (as in (4.7)) vanishes in the limit
$U_1^*$ (as in (4.7)) vanishes in the limit ![]() $Re\to 0$. Hence, we treat
$Re\to 0$. Hence, we treat ![]() $U_1$ (as in (4.6)) as the corrected migration velocity
$U_1$ (as in (4.6)) as the corrected migration velocity ![]() $U$ at
$U$ at ![]() $O(Re)$ for the sake of concurrence of the velocity field and the associated swimming characteristics in the limit
$O(Re)$ for the sake of concurrence of the velocity field and the associated swimming characteristics in the limit ![]() $Re\to 0$.
$Re\to 0$.
4.2. Migration velocity
In the absence of inertial effect, i.e. in ![]() $Re\to 0$ limit, the locomotion speed of the droplet is essentially controlled by the first mode of the surface stress activity. However, (4.6) implies that the second mode of the induced stress field plays a predominant role in the migration velocity of the droplet for finite Reynolds numbers. In figure 2(a), the variation of
$Re\to 0$ limit, the locomotion speed of the droplet is essentially controlled by the first mode of the surface stress activity. However, (4.6) implies that the second mode of the induced stress field plays a predominant role in the migration velocity of the droplet for finite Reynolds numbers. In figure 2(a), the variation of ![]() $U$ with the Reynolds number
$U$ with the Reynolds number ![]() $Re$ has been depicted for a set of
$Re$ has been depicted for a set of ![]() $\sigma$ values. Typically, the inertial effect of the medium reduces the viscous resistance for the droplet and hence the migration velocity is enhanced. In pursuance of comparison with the low Reynolds number characteristics of the squirmers, which is the classical model for analysing the migration of micro-swimmers, a straightforward analysis of the surface flows and the associated stresslet strength of any Marangoni stress-driven flow will imply that
$\sigma$ values. Typically, the inertial effect of the medium reduces the viscous resistance for the droplet and hence the migration velocity is enhanced. In pursuance of comparison with the low Reynolds number characteristics of the squirmers, which is the classical model for analysing the migration of micro-swimmers, a straightforward analysis of the surface flows and the associated stresslet strength of any Marangoni stress-driven flow will imply that ![]() $\beta = \beta _2/\beta _1 \sim -\sigma _2/\sigma _1$ (Schmitt & Stark Reference Schmitt and Stark2016b). For squirmers using purely tangential velocity actuation, one can categorize the swimmer as neutral when
$\beta = \beta _2/\beta _1 \sim -\sigma _2/\sigma _1$ (Schmitt & Stark Reference Schmitt and Stark2016b). For squirmers using purely tangential velocity actuation, one can categorize the swimmer as neutral when ![]() $\beta =0$, a pusher (or puller) when
$\beta =0$, a pusher (or puller) when ![]() $\beta$ is negative (or positive). This can be verified by the swimming patterns observed in figure 3 where the streamlines for
$\beta$ is negative (or positive). This can be verified by the swimming patterns observed in figure 3 where the streamlines for ![]() $\sigma =-5$ are analogous to the swimming pattern of a puller (
$\sigma =-5$ are analogous to the swimming pattern of a puller (![]() $\beta >0$) and vice versa.
$\beta >0$) and vice versa.
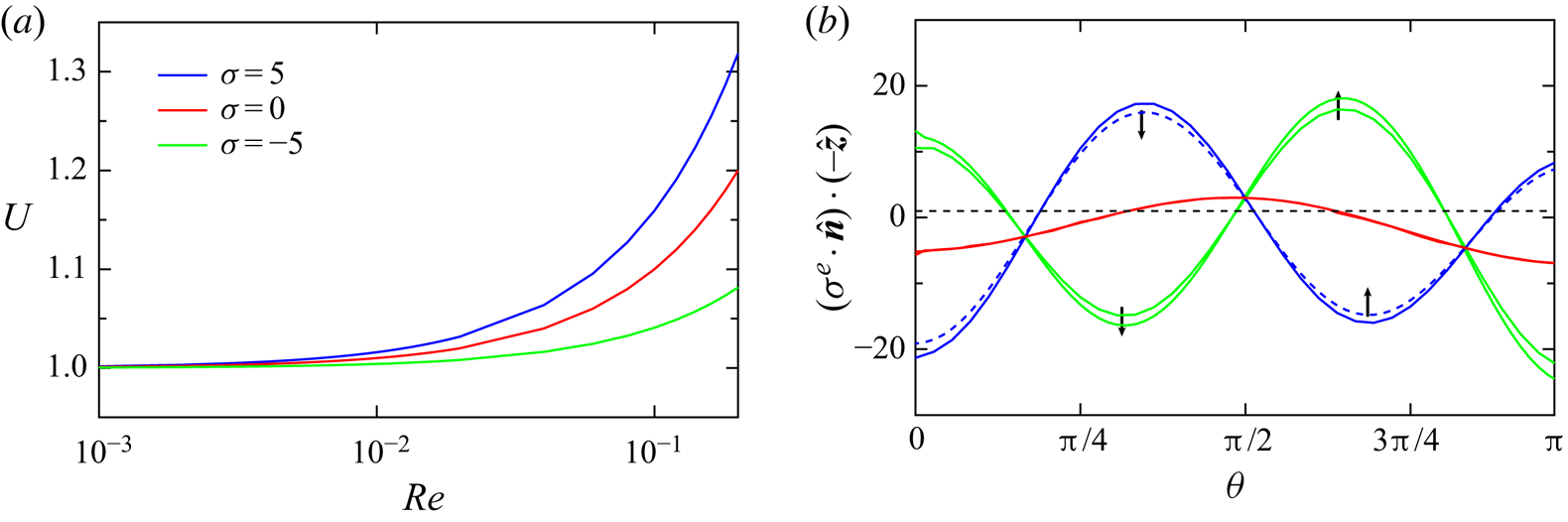
Figure 2. ![]() $(a)$ The dimensionless migration velocity (
$(a)$ The dimensionless migration velocity (![]() $U$) as a function of
$U$) as a function of ![]() $Re$, for different
$Re$, for different ![]() $\sigma$ values fixing
$\sigma$ values fixing ![]() $\sigma _1=1$ and
$\sigma _1=1$ and ![]() $\lambda =0.5$. We have varied
$\lambda =0.5$. We have varied ![]() $Re$ in such a way that the conditions
$Re$ in such a way that the conditions ![]() $\sigma Re<1$,
$\sigma Re<1$, ![]() $\sigma Re \lambda <1$ and
$\sigma Re \lambda <1$ and ![]() $\sigma Re \lambda ^2<1$ are satisfied.
$\sigma Re \lambda ^2<1$ are satisfied. ![]() $(b)$ The variation of the surface stress of the spherical droplet swimmer, in the direction of migration, as a function of polar angle
$(b)$ The variation of the surface stress of the spherical droplet swimmer, in the direction of migration, as a function of polar angle ![]() $\theta$ for different
$\theta$ for different ![]() $\sigma$ values. The solid and dashed lines (green
$\sigma$ values. The solid and dashed lines (green ![]() $\&$ blue) represent the stress variation for
$\&$ blue) represent the stress variation for ![]() $Re=0$ and
$Re=0$ and ![]() $Re=0.19$, respectively. For
$Re=0.19$, respectively. For ![]() $\sigma =0$, the solid and dashed lines coincide.
$\sigma =0$, the solid and dashed lines coincide.
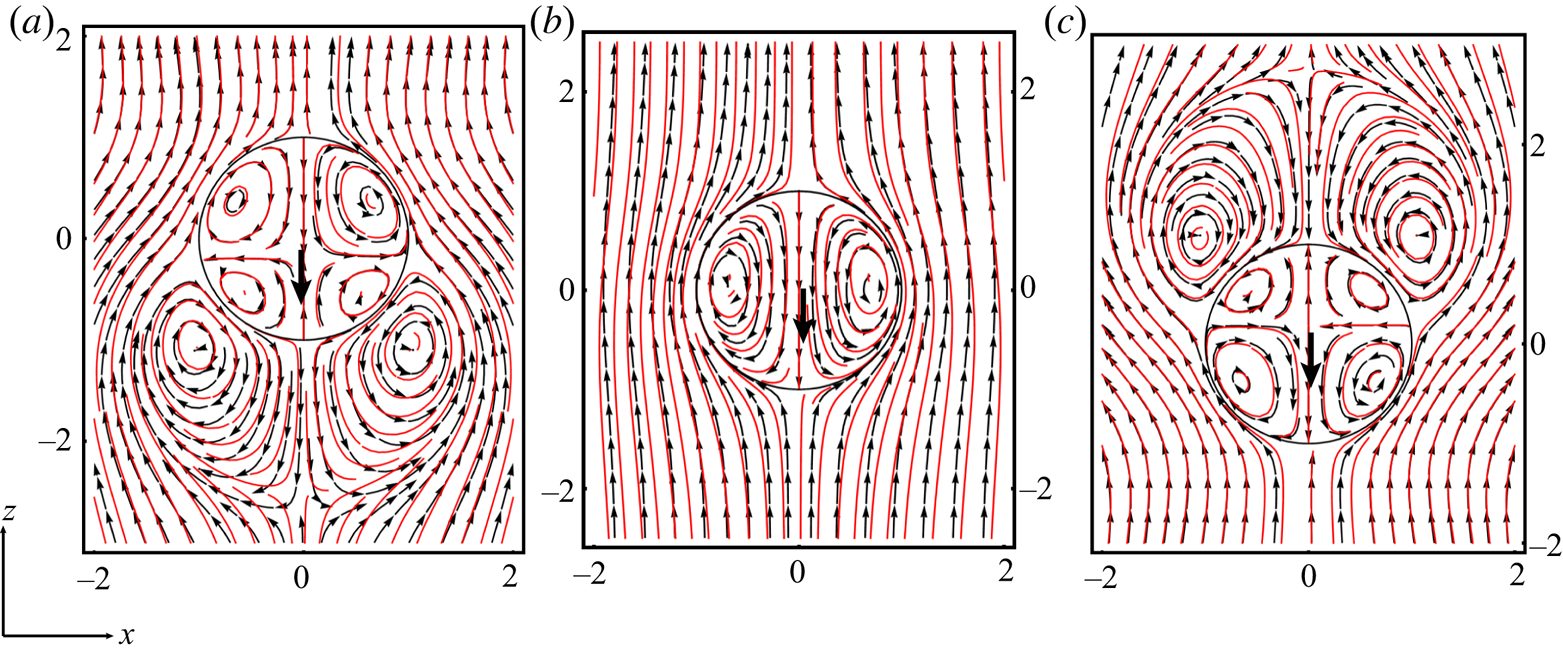
Figure 3. The comparison of the streamlines of the velocity field of the droplet swimmer with ![]() $(a)$
$(a)$ ![]() $\sigma =5$,
$\sigma =5$, ![]() $(b)$
$(b)$ ![]() $\sigma = 0$ and
$\sigma = 0$ and ![]() $(c)$
$(c)$ ![]() $\sigma =-5$. The red lines and the black arrow lines represents the streamlines for
$\sigma =-5$. The red lines and the black arrow lines represents the streamlines for ![]() $Re=0.19$ and the
$Re=0.19$ and the ![]() $Re=0$ limit, respectively at
$Re=0$ limit, respectively at ![]() $\lambda =0.5$. The solid black arrow indicates the direction of the migration.
$\lambda =0.5$. The solid black arrow indicates the direction of the migration.
For solid squirmers, pushers (![]() $\beta <0$) have their locomotion speed increased while for pullers (
$\beta <0$) have their locomotion speed increased while for pullers (![]() $\beta >0$), the speed decreases with
$\beta >0$), the speed decreases with ![]() $Re$. Further, for a neutral (
$Re$. Further, for a neutral (![]() $\beta =0$) squirmer stresslets are absent in the external medium; hence, the migration velocity remains unaltered by
$\beta =0$) squirmer stresslets are absent in the external medium; hence, the migration velocity remains unaltered by ![]() $Re$ (Wang & Ardekani Reference Wang and Ardekani2011). In contrast, the observation that the migration velocity of a swimming droplet exhibits an increasing trend with
$Re$ (Wang & Ardekani Reference Wang and Ardekani2011). In contrast, the observation that the migration velocity of a swimming droplet exhibits an increasing trend with ![]() $Re$ for any value of
$Re$ for any value of ![]() $\sigma$ is intriguing. Similar to a neutral squirmer, for
$\sigma$ is intriguing. Similar to a neutral squirmer, for ![]() $\sigma =0$, due to the absence of vortices in the exterior medium, the interfacial stress in the direction of migration (i.e. negative
$\sigma =0$, due to the absence of vortices in the exterior medium, the interfacial stress in the direction of migration (i.e. negative ![]() $z$-direction) remains unaltered at finite
$z$-direction) remains unaltered at finite ![]() $Re$ (see figure 2b). However, for droplets with
$Re$ (see figure 2b). However, for droplets with ![]() ${\sigma =0}$, vortices are formed interior to the droplet, which gets redistributed due to the inertial effects (see figure 3b). Therefore, the migration velocity evolves with
${\sigma =0}$, vortices are formed interior to the droplet, which gets redistributed due to the inertial effects (see figure 3b). Therefore, the migration velocity evolves with ![]() $Re$. Straightaway, from (4.6) we note that the subsequent increase from the neutral case is relatively higher or lower for
$Re$. Straightaway, from (4.6) we note that the subsequent increase from the neutral case is relatively higher or lower for ![]() $\sigma >0$ or
$\sigma >0$ or ![]() $\sigma <0$, respectively. Figure 3(a) depicts that, for
$\sigma <0$, respectively. Figure 3(a) depicts that, for ![]() $\sigma =5$, the stresslets or the closed-streamline re-circulatory regions of the external fluid, developed in the direction of the migration, get abbreviated due to finite inertial effects. Subsequently, the interfacial stress in the direction of migration gets reduced for
$\sigma =5$, the stresslets or the closed-streamline re-circulatory regions of the external fluid, developed in the direction of the migration, get abbreviated due to finite inertial effects. Subsequently, the interfacial stress in the direction of migration gets reduced for ![]() $\sigma >0$ (see figure 2b) and the migration velocity increases significantly, identical to the behaviour of an equivalent squirmer (with
$\sigma >0$ (see figure 2b) and the migration velocity increases significantly, identical to the behaviour of an equivalent squirmer (with ![]() $\beta <0$). Surprisingly for
$\beta <0$). Surprisingly for ![]() $\sigma =-5$, although the external stresslets enlarge due to inertial effect, which successively enhances the interfacial stress (see figure 2b), the migration velocity increases with
$\sigma =-5$, although the external stresslets enlarge due to inertial effect, which successively enhances the interfacial stress (see figure 2b), the migration velocity increases with ![]() $Re$. This is due to the existence of prominent counter rotating vortices of the interior flow in the direction of migration of the droplet (see figure 3c), which re-acclimate and retaliate the enhanced stress at finite
$Re$. This is due to the existence of prominent counter rotating vortices of the interior flow in the direction of migration of the droplet (see figure 3c), which re-acclimate and retaliate the enhanced stress at finite ![]() $Re$ (Mason & Moremedi Reference Mason and Moremedi2011). In this regard, we note that the previous counteraction for
$Re$ (Mason & Moremedi Reference Mason and Moremedi2011). In this regard, we note that the previous counteraction for ![]() $\sigma <0$ is inconceivable for an equivalent solid squirmer (with
$\sigma <0$ is inconceivable for an equivalent solid squirmer (with ![]() $\beta >0$). This alludes to the fact that the droplet swimmers are more malleable at finite
$\beta >0$). This alludes to the fact that the droplet swimmers are more malleable at finite ![]() $Re$ than its rigid counterparts.
$Re$ than its rigid counterparts.
Furthermore, as a consequence of truncation up to ![]() $\lambda ^2$, we observe that
$\lambda ^2$, we observe that ![]() $Re$ quadratically couples with
$Re$ quadratically couples with ![]() $\lambda$ and
$\lambda$ and ![]() $\sigma$ (see (4.6)). Correspondingly, the magnitude of net migration velocity
$\sigma$ (see (4.6)). Correspondingly, the magnitude of net migration velocity ![]() $(-2 \sigma _1 \lambda /(3 (3+2 \lambda )) \, U$ increases monotonically as a function of
$(-2 \sigma _1 \lambda /(3 (3+2 \lambda )) \, U$ increases monotonically as a function of ![]() $\lambda$ (within the limit
$\lambda$ (within the limit ![]() $\lambda <1$) with escalation governed by the choice of
$\lambda <1$) with escalation governed by the choice of ![]() $\sigma$ at
$\sigma$ at ![]() $O(Re)$. This is identical to the qualitative behaviour of
$O(Re)$. This is identical to the qualitative behaviour of ![]() $U$ vs.
$U$ vs. ![]() $\lambda$ in the limit
$\lambda$ in the limit ![]() $Re\to 0$. Overall, the above results highlight the fact that within the insisted range
$Re\to 0$. Overall, the above results highlight the fact that within the insisted range ![]() $\lambda <1$ the inertial effect of a droplet is invariably lower than the external fluid, therefore both
$\lambda <1$ the inertial effect of a droplet is invariably lower than the external fluid, therefore both ![]() $Re$ and
$Re$ and ![]() $\lambda$ synergistically enhance the locomotion speed of the droplet swimmer, and a keen choice of
$\lambda$ synergistically enhance the locomotion speed of the droplet swimmer, and a keen choice of ![]() $\sigma$ determines the percentage increase.
$\sigma$ determines the percentage increase.
4.3. Power dissipation and efficiency
Primarily, the rate of work done by the swimmer can be quantified by ![]() $P=-\int (\boldsymbol {\varSigma ^e} \boldsymbol {\cdot } \boldsymbol {\hat {n}}) \boldsymbol {\cdot } \boldsymbol {v^e}\,\textrm {d}s$, which can be calculated with the help of constitutive relations and the corresponding flow fields of the swimmer. Additionally, using the reciprocal theorem, the viscous dissipation of a spherical body with purely tangential surface activity can be written in terms of the vorticity and the surface velocity of the swimmer (Stone & Samuel Reference Stone and Samuel1996; Masoud & Stone Reference Masoud and Stone2019). Following this, one may infer that with increasing
$P=-\int (\boldsymbol {\varSigma ^e} \boldsymbol {\cdot } \boldsymbol {\hat {n}}) \boldsymbol {\cdot } \boldsymbol {v^e}\,\textrm {d}s$, which can be calculated with the help of constitutive relations and the corresponding flow fields of the swimmer. Additionally, using the reciprocal theorem, the viscous dissipation of a spherical body with purely tangential surface activity can be written in terms of the vorticity and the surface velocity of the swimmer (Stone & Samuel Reference Stone and Samuel1996; Masoud & Stone Reference Masoud and Stone2019). Following this, one may infer that with increasing ![]() $Re$, the droplet that minimizes the vorticity will also minimize the power dissipation. Figure 4(a) illustrates this trend. The vortices in the vicinity of the droplet when
$Re$, the droplet that minimizes the vorticity will also minimize the power dissipation. Figure 4(a) illustrates this trend. The vortices in the vicinity of the droplet when ![]() $\sigma <0$ get outweighed for non-zero
$\sigma <0$ get outweighed for non-zero ![]() $Re$, which enhance the corresponding dissipated power with increasing
$Re$, which enhance the corresponding dissipated power with increasing ![]() $Re$. Nevertheless, for
$Re$. Nevertheless, for ![]() $\sigma \geq 0$, the dissipated power decreases monotonically due to abbreviation or redistribution of the external or internal vortices, respectively. One might conjecture that this behaviour contradicts the Helmholtz minimum dissipation theorem (Batchelor Reference Batchelor1967), which guarantees that a Stokes flow field dissipates less energy than any other incompressible flow field with the same boundary velocities. However, the theorem does not apply here as the far-field boundary velocity is denoted by the migration velocity of the droplet which depends on Reynolds number.
$\sigma \geq 0$, the dissipated power decreases monotonically due to abbreviation or redistribution of the external or internal vortices, respectively. One might conjecture that this behaviour contradicts the Helmholtz minimum dissipation theorem (Batchelor Reference Batchelor1967), which guarantees that a Stokes flow field dissipates less energy than any other incompressible flow field with the same boundary velocities. However, the theorem does not apply here as the far-field boundary velocity is denoted by the migration velocity of the droplet which depends on Reynolds number.
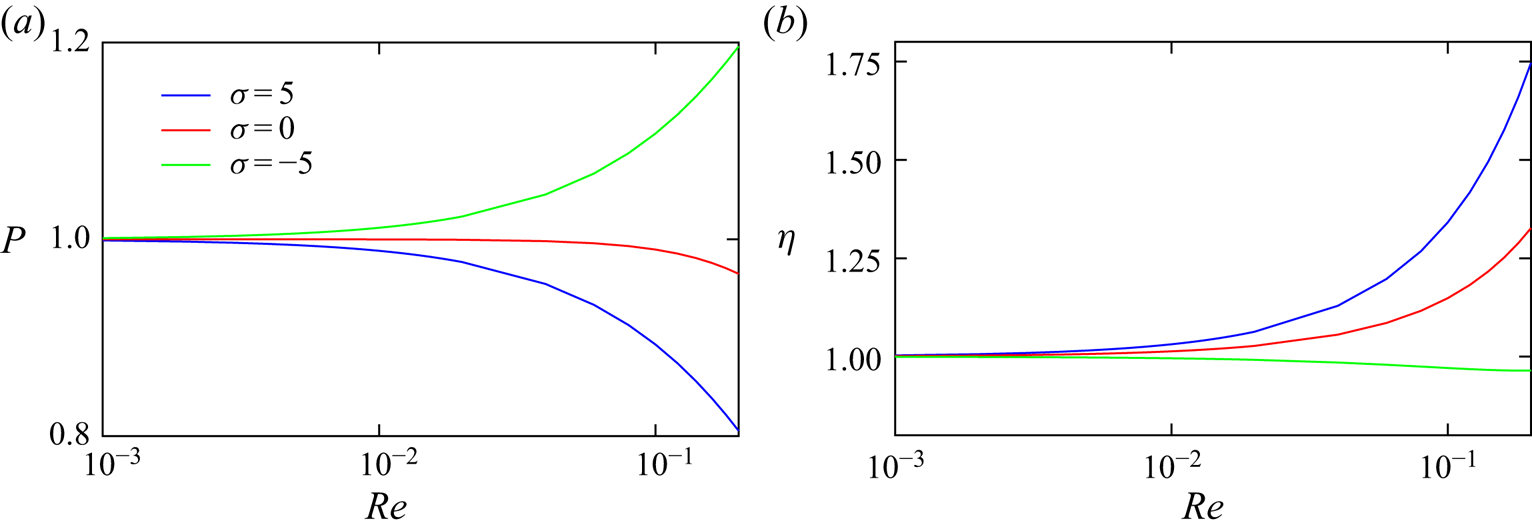
Figure 4. ![]() $(a)$ The power dissipation and
$(a)$ The power dissipation and ![]() $(b)$ the corresponding efficiency of the droplet swimmer as a function of the Reynolds number
$(b)$ the corresponding efficiency of the droplet swimmer as a function of the Reynolds number ![]() $Re$ for different
$Re$ for different ![]() $\sigma$ values fixing
$\sigma$ values fixing ![]() $\sigma _1=1$ and
$\sigma _1=1$ and ![]() $\lambda =0.5$. Here, the absolute power and efficiency of the droplet are scaled with the respective values at
$\lambda =0.5$. Here, the absolute power and efficiency of the droplet are scaled with the respective values at ![]() $Re \to 0$ limit, i.e.
$Re \to 0$ limit, i.e. ![]() $P \to P/P_{Re\to 0}$ and
$P \to P/P_{Re\to 0}$ and ![]() $\eta \to \eta /\eta _{Re \to 0}$.
$\eta \to \eta /\eta _{Re \to 0}$.
While the energetic cost of moving through a medium is an essential property of locomotion, for self-propelling systems, it is relevant to investigate how the properties of the swimmer and the surrounding medium influence the efficiency of the locomotion. According to Lighthill (Reference Lighthill1952), the efficiency (![]() $\eta$) of a swimmer is defined as the ratio of the power necessary to pull the swimmer at the swimming speed (i.e.
$\eta$) of a swimmer is defined as the ratio of the power necessary to pull the swimmer at the swimming speed (i.e. ![]() $F_H\, U$) to the rate of work done (
$F_H\, U$) to the rate of work done (![]() $P$) by the swimmer, i.e.
$P$) by the swimmer, i.e. ![]() $\eta =F_H\,U/P$. Here, we consider
$\eta =F_H\,U/P$. Here, we consider ![]() $F_H$ as the hydrodynamic force acting on the spherical droplet at
$F_H$ as the hydrodynamic force acting on the spherical droplet at ![]() $O(Re)$ limit, which is given by (Taylor & Acrivos Reference Taylor and Acrivos1964)
$O(Re)$ limit, which is given by (Taylor & Acrivos Reference Taylor and Acrivos1964)
Note that ![]() $F_{H}$ also represents the Hadamard and Rybczynski drag force of a droplet in the limit
$F_{H}$ also represents the Hadamard and Rybczynski drag force of a droplet in the limit ![]() $Re\to 0$ (Clift, Grace & Weber Reference Clift, Grace and Weber1978; Sadhal, Ayyaswamy & Chung Reference Sadhal, Ayyaswamy and Chung1997). The above expression agrees with the well-established low Reynolds number drag of a solid sphere in the limit
$Re\to 0$ (Clift, Grace & Weber Reference Clift, Grace and Weber1978; Sadhal, Ayyaswamy & Chung Reference Sadhal, Ayyaswamy and Chung1997). The above expression agrees with the well-established low Reynolds number drag of a solid sphere in the limit ![]() $\lambda \to 0$ (Proudman & Pearson Reference Proudman and Pearson1957). Note that the swimming efficiency is systematically higher over the entire range of
$\lambda \to 0$ (Proudman & Pearson Reference Proudman and Pearson1957). Note that the swimming efficiency is systematically higher over the entire range of ![]() $Re$ (see figure 4b) for
$Re$ (see figure 4b) for ![]() $\sigma >0$ and
$\sigma >0$ and ![]() $\sigma =0$. It would be reasonable to expect that droplets with
$\sigma =0$. It would be reasonable to expect that droplets with ![]() $\sigma >0$ are more efficient than the droplets with
$\sigma >0$ are more efficient than the droplets with ![]() $\sigma=0$. Notably, for
$\sigma=0$. Notably, for ![]() $\sigma =5$,
$\sigma =5$, ![]() $\eta$ is significantly pronounced (more than 1.5 times) in the limit
$\eta$ is significantly pronounced (more than 1.5 times) in the limit ![]() $\sigma Re <1$, whereas for
$\sigma Re <1$, whereas for ![]() $\sigma =-5$ the efficiency meagrely reduces due to higher power consumption at
$\sigma =-5$ the efficiency meagrely reduces due to higher power consumption at ![]() $O(Re)$. Although for
$O(Re)$. Although for ![]() $\sigma <0$,
$\sigma <0$, ![]() $U$ increases as a function of
$U$ increases as a function of ![]() $Re$, the output power
$Re$, the output power ![]() $F_H U$ under performs the dissipated power
$F_H U$ under performs the dissipated power ![]() $P$, which further decreases the efficiency. This reinforces the fact that for a broader class of droplets (
$P$, which further decreases the efficiency. This reinforces the fact that for a broader class of droplets (![]() $\sigma \geq 0$) swimming against fully resistive viscous medium is challenging and less efficient (Purcell Reference Purcell1977). When inertia is present, the droplets (
$\sigma \geq 0$) swimming against fully resistive viscous medium is challenging and less efficient (Purcell Reference Purcell1977). When inertia is present, the droplets (![]() $\sigma \geq 0$) effectively exploit the depleted viscous resistance from the external medium to gain higher motility as well as energetically efficient swimming. This finding is analogous to the efficiency of a solid squirmer in a low Reynolds number flow.
$\sigma \geq 0$) effectively exploit the depleted viscous resistance from the external medium to gain higher motility as well as energetically efficient swimming. This finding is analogous to the efficiency of a solid squirmer in a low Reynolds number flow.
Moreover, our results reveal some noticeable observations on the behaviour of ![]() $P$ and
$P$ and ![]() $\eta$ with respect to the viscosity ratio
$\eta$ with respect to the viscosity ratio ![]() $\lambda$ at finite
$\lambda$ at finite ![]() $Re$. Recall that for a droplet with
$Re$. Recall that for a droplet with ![]() $\sigma =0$, no additional
$\sigma =0$, no additional ![]() $\lambda$ dependency is witnessed in the corrected migration velocity
$\lambda$ dependency is witnessed in the corrected migration velocity ![]() $\tilde {U}$ (see (4.6)). Consequently, all the associated swimming properties necessarily follow the corresponding Stokesian behaviour (i.e. at
$\tilde {U}$ (see (4.6)). Consequently, all the associated swimming properties necessarily follow the corresponding Stokesian behaviour (i.e. at ![]() $Re \to 0$) with
$Re \to 0$) with ![]() $\lambda$. Interestingly, for
$\lambda$. Interestingly, for ![]() $\sigma >0$, the Stokesian behaviour also persists with increasing
$\sigma >0$, the Stokesian behaviour also persists with increasing ![]() $\lambda$ at
$\lambda$ at ![]() $O(Re)$ despite an acquired
$O(Re)$ despite an acquired ![]() $\lambda ^2$ reliance. Subsequently, we observe
$\lambda ^2$ reliance. Subsequently, we observe ![]() $P$ (or
$P$ (or ![]() $\eta$) monotonically decreases (or increases) with
$\eta$) monotonically decreases (or increases) with ![]() $\lambda$ in the limit
$\lambda$ in the limit ![]() $\lambda < 1$ (see figure 5). However, for
$\lambda < 1$ (see figure 5). However, for ![]() $\sigma <0$, as mentioned earlier that the stresslets generated by the swimmer intensify due to the inertial effect. Consequently, the apparent extent of the swimmer (i.e. swimmer with the associated vortices) increases at finite
$\sigma <0$, as mentioned earlier that the stresslets generated by the swimmer intensify due to the inertial effect. Consequently, the apparent extent of the swimmer (i.e. swimmer with the associated vortices) increases at finite ![]() $Re$. Therefore, towards higher
$Re$. Therefore, towards higher ![]() $\lambda$ (within the limit
$\lambda$ (within the limit ![]() $\lambda < 1$) the Reynolds number associated with the internal fluid becomes comparable to the Reynolds number of the external fluid. Consequently, the swimmer with
$\lambda < 1$) the Reynolds number associated with the internal fluid becomes comparable to the Reynolds number of the external fluid. Consequently, the swimmer with ![]() $\sigma <0$ dissipates lower power (
$\sigma <0$ dissipates lower power (![]() $P$) and exhibits higher efficiency (
$P$) and exhibits higher efficiency (![]() $\eta$) towards higher
$\eta$) towards higher ![]() $\lambda$ and the foreseen increasing (or decreasing) trend for
$\lambda$ and the foreseen increasing (or decreasing) trend for ![]() $\eta$ (or
$\eta$ (or ![]() $P$) discontinues at higher
$P$) discontinues at higher ![]() $\lambda$ (see figure 5).
$\lambda$ (see figure 5).
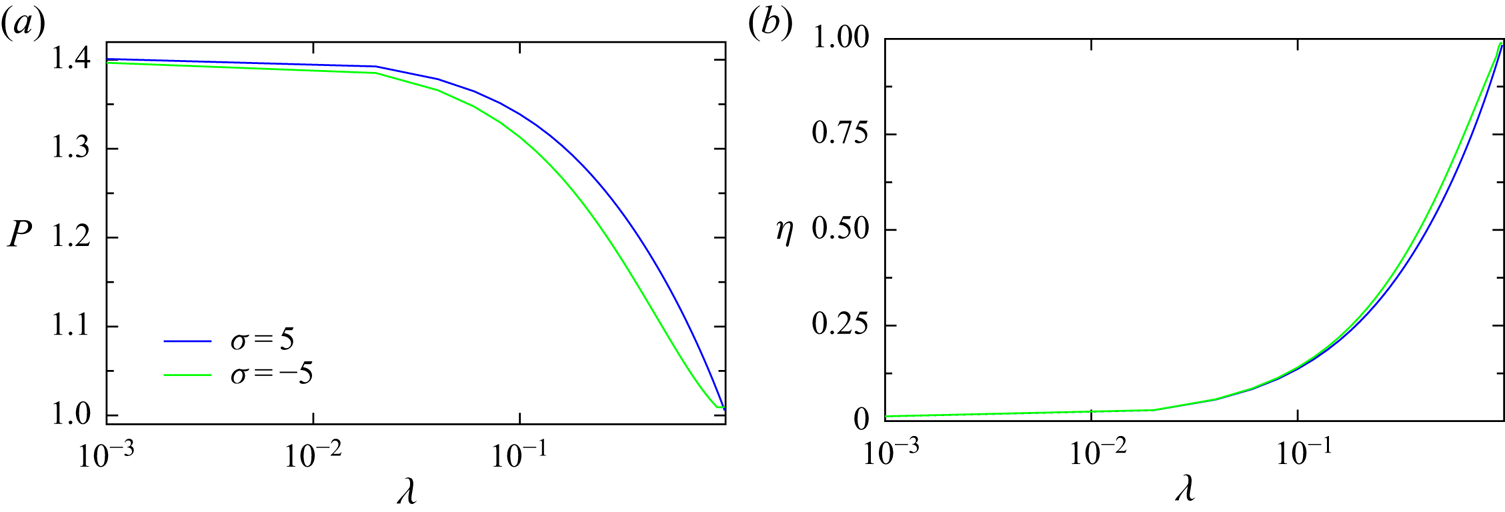
Figure 5. ![]() $(a)$ The power dissipation and
$(a)$ The power dissipation and ![]() $(b)$ the corresponding efficiency of the droplet swimmer as a function of the viscosity ratio
$(b)$ the corresponding efficiency of the droplet swimmer as a function of the viscosity ratio ![]() $\lambda$ for different
$\lambda$ for different ![]() $\sigma$ values at
$\sigma$ values at ![]() $Re=0.19$. Here, the absolute power and efficiency of the droplet are scaled as
$Re=0.19$. Here, the absolute power and efficiency of the droplet are scaled as ![]() $P \to P/P_{\lambda \to 1}$ and
$P \to P/P_{\lambda \to 1}$ and ![]() $\eta \to \eta /\eta _{\lambda \to 1}$, respectively.
$\eta \to \eta /\eta _{\lambda \to 1}$, respectively.
4.4. Linear stability analysis of the migration
In the preceding section, we have shown the impact of the inertial effect on the self-propulsion of the droplet with inhomogeneous surface tension. Towards this, we have asserted the dimensionless velocity ![]() $U=U_1$ as the coherent solution at
$U=U_1$ as the coherent solution at ![]() $O(Re)$. However, the present system incorporates the nonlinear convective inertial effects of the surrounding medium; this persuades the investigation of the linear stability of drag function
$O(Re)$. However, the present system incorporates the nonlinear convective inertial effects of the surrounding medium; this persuades the investigation of the linear stability of drag function ![]() $D$ derived in (4.5). Figure 6 illustrates the fixed points of the drag function
$D$ derived in (4.5). Figure 6 illustrates the fixed points of the drag function ![]() $D$, which mark the migration velocities
$D$, which mark the migration velocities ![]() $U_1$ and
$U_1$ and ![]() $U_1^*$. We perform the linear stability analysis around the fixed points. We analyse the first derivative of the drag function
$U_1^*$. We perform the linear stability analysis around the fixed points. We analyse the first derivative of the drag function ![]() $D$ at
$D$ at ![]() $U_1$ and
$U_1$ and ![]() $U_1^*$, which measures the rate of decay to the corresponding fixed points. Further investigation indicates that at
$U_1^*$, which measures the rate of decay to the corresponding fixed points. Further investigation indicates that at ![]() $U=U_1$,
$U=U_1$, ![]() $\partial D/\partial U>0$, whereas at
$\partial D/\partial U>0$, whereas at ![]() $U=U_1^*$, we have
$U=U_1^*$, we have ![]() $\partial D/\partial U<0$ for all
$\partial D/\partial U<0$ for all ![]() $\sigma$ values. Interestingly, the negative slope at the latter fixed point establishes
$\sigma$ values. Interestingly, the negative slope at the latter fixed point establishes ![]() $U=U_1^*$ as an asymptotically stable swimming state of the droplet swimmer, which corresponds to zero migration in
$U=U_1^*$ as an asymptotically stable swimming state of the droplet swimmer, which corresponds to zero migration in ![]() $Re\to 0$ limit. This can be understood as follows.
$Re\to 0$ limit. This can be understood as follows.
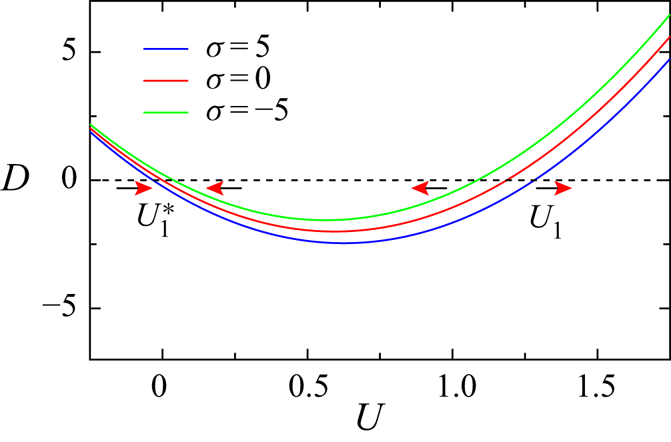
Figure 6. The nonlinear drag function ![]() $D$ ((4.5)) as a function of the dimensionless migration velocity
$D$ ((4.5)) as a function of the dimensionless migration velocity ![]() $U$ at
$U$ at ![]() $Re=0.19$,
$Re=0.19$, ![]() $\lambda =0.5$, and at different
$\lambda =0.5$, and at different ![]() $\sigma$ values.
$\sigma$ values. ![]() $U_1$ and
$U_1$ and ![]() $U_1^*$ are the fixed points of the function. The arrows indicate the trend of the function near the fixed points, which also demonstrates the stability.
$U_1^*$ are the fixed points of the function. The arrows indicate the trend of the function near the fixed points, which also demonstrates the stability.
The external sources for inhomogeneous surface tension i.e. external thermal or chemical gradients, or inhomogeneous coverage of surfactant molecules reduce the local interfacial tension (![]() $\gamma$), developing the Marangoni flow towards the higher
$\gamma$), developing the Marangoni flow towards the higher ![]() $\gamma$ value. However, the Marangoni flow across the interface induces a short-lived motion of the droplet. In the absence of external forces, neglecting the inertial effect of the medium, the long-time limit leads to an equilibrium state of the droplet. This corresponds to no migration as the droplet achieves a state of uniform interfacial tension (Izri et al. Reference Izri, van der Linden, Michelin and Dauchot2014). Nevertheless, for low but finite Reynolds number due to nonlinear convective effect of the surroundings, we proclaim that at a later stage the velocity of the droplet decreases from the initial velocity
$\gamma$ value. However, the Marangoni flow across the interface induces a short-lived motion of the droplet. In the absence of external forces, neglecting the inertial effect of the medium, the long-time limit leads to an equilibrium state of the droplet. This corresponds to no migration as the droplet achieves a state of uniform interfacial tension (Izri et al. Reference Izri, van der Linden, Michelin and Dauchot2014). Nevertheless, for low but finite Reynolds number due to nonlinear convective effect of the surroundings, we proclaim that at a later stage the velocity of the droplet decreases from the initial velocity ![]() $U_1$ and develops a distinct migration velocity
$U_1$ and develops a distinct migration velocity ![]() $U_1^*$ before impending the halt. This asymptotically stable migration velocity is an outcome of the nonlinear interaction of the droplet with the surrounding medium and is dictated by the Reynolds number
$U_1^*$ before impending the halt. This asymptotically stable migration velocity is an outcome of the nonlinear interaction of the droplet with the surrounding medium and is dictated by the Reynolds number ![]() $Re$ and the choice of
$Re$ and the choice of ![]() $\sigma$. For
$\sigma$. For ![]() $\sigma =0$,
$\sigma =0$, ![]() $U_1^*$ is zero but for
$U_1^*$ is zero but for ![]() $\sigma >0$ or
$\sigma >0$ or ![]() $\sigma <0$ it indicates a migration in positive or negative
$\sigma <0$ it indicates a migration in positive or negative ![]() $z$-direction, respectively. Interestingly, this refers to a plausible reversal of the migration direction from the migration induced by
$z$-direction, respectively. Interestingly, this refers to a plausible reversal of the migration direction from the migration induced by ![]() $U=U_1$ for
$U=U_1$ for ![]() $\sigma >0$. However, our aim is to analyse the droplet in its early unsettled phase. Therefore, in the present framework, all the swimming characteristics are analysed employing the migration velocity
$\sigma >0$. However, our aim is to analyse the droplet in its early unsettled phase. Therefore, in the present framework, all the swimming characteristics are analysed employing the migration velocity ![]() $U=U_1$.
$U=U_1$.
5. Second-order migration velocity
In order to derive an expression for a migration velocity up to ![]() $O(Re^2)$, we stress that the net drag experienced by the droplet up to the same order must vanish across the surface. By employing the expression of the approximated streamfunction
$O(Re^2)$, we stress that the net drag experienced by the droplet up to the same order must vanish across the surface. By employing the expression of the approximated streamfunction ![]() $\psi _2^e$ as in (3.25), we follow an equivalent formalism as summarized in § 4. A lengthy and strenuous analysis shows that
$\psi _2^e$ as in (3.25), we follow an equivalent formalism as summarized in § 4. A lengthy and strenuous analysis shows that
where ![]() $A$,
$A$, ![]() $B$, and
$B$, and ![]() $C$ are obtained as
$C$ are obtained as
 \begin{equation} \left. \begin{array}{c@{}} A = 0.134 -0.064 \lambda + 0.066 \lambda^2, \\ B = 0.443 -0.403 \lambda + 0.995 \lambda^2, \\ C = 0.0024 + 0.0035 \lambda - 0.0085 \lambda^2. \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{c@{}} A = 0.134 -0.064 \lambda + 0.066 \lambda^2, \\ B = 0.443 -0.403 \lambda + 0.995 \lambda^2, \\ C = 0.0024 + 0.0035 \lambda - 0.0085 \lambda^2. \end{array} \right\} \end{equation} It may be noted that, throughout the analysis, by maintaining the ![]() $\lambda <1$ limit, we have considered terms up to
$\lambda <1$ limit, we have considered terms up to ![]() $\lambda ^2$. Likewise, we argue that the strengths of
$\lambda ^2$. Likewise, we argue that the strengths of ![]() $Re^2\lambda \sigma$,
$Re^2\lambda \sigma$, ![]() $Re^2\lambda \sigma ^2$,
$Re^2\lambda \sigma ^2$, ![]() $Re^2\lambda ^2\sigma$ and
$Re^2\lambda ^2\sigma$ and ![]() $Re^2\lambda ^2\sigma ^2$ are less than unity in the present analysis;
$Re^2\lambda ^2\sigma ^2$ are less than unity in the present analysis; ![]() $U$ in (5.1) represents the real and coherent solution at
$U$ in (5.1) represents the real and coherent solution at ![]() $O(Re^2)$. In figure 7, a direct comparison of the swimming velocities as in (4.6) and (5.1) reveals that in the limit
$O(Re^2)$. In figure 7, a direct comparison of the swimming velocities as in (4.6) and (5.1) reveals that in the limit ![]() $Re < 1$, as
$Re < 1$, as ![]() $U$ in (5.1) is viewed as quadratic power series of
$U$ in (5.1) is viewed as quadratic power series of ![]() $Re$, it inherently predicts a higher upsurge of the migration velocity for both
$Re$, it inherently predicts a higher upsurge of the migration velocity for both ![]() $\sigma >0$ and
$\sigma >0$ and ![]() $\sigma <0$. Table 1 illustrates the quantitative increase (
$\sigma <0$. Table 1 illustrates the quantitative increase (![]() $U-1$) of migration velocity with growing perturbations in Reynolds number. The conclusion from table 1 is that the difference between
$U-1$) of migration velocity with growing perturbations in Reynolds number. The conclusion from table 1 is that the difference between ![]() $O(Re)$ and
$O(Re)$ and ![]() $O(Re^2)$ is prominent in the range
$O(Re^2)$ is prominent in the range ![]() $Re \sim 10^{-1}$ at which the inertial effect is evident in the inner regime. Interestingly, we note that for a particular case when
$Re \sim 10^{-1}$ at which the inertial effect is evident in the inner regime. Interestingly, we note that for a particular case when ![]() $C=0$ the contribution of the
$C=0$ the contribution of the ![]() $\sigma ^2$ is nullified in the migration velocity. Consequently, the disparity between
$\sigma ^2$ is nullified in the migration velocity. Consequently, the disparity between ![]() $O(Re)$ and
$O(Re)$ and ![]() $O(Re^2)$ is curtailed reasonably.
$O(Re^2)$ is curtailed reasonably.
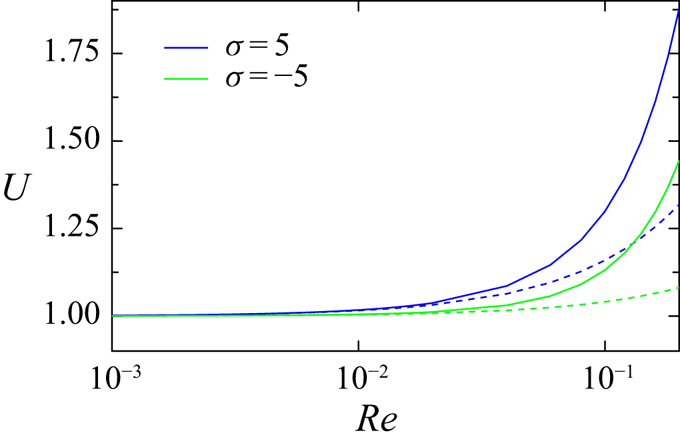
Figure 7. The comparison between the first-order (![]() $O(Re)$) (dashed line) and second-order (
$O(Re)$) (dashed line) and second-order (![]() $O(Re^2)$) (solid line) migration velocity with the Reynolds number for both
$O(Re^2)$) (solid line) migration velocity with the Reynolds number for both ![]() $\sigma =5$ and
$\sigma =5$ and ![]() $\sigma =-5$ at
$\sigma =-5$ at ![]() $\lambda =0.5$. As envisaged, the augmentations for both the cases are considerably higher for
$\lambda =0.5$. As envisaged, the augmentations for both the cases are considerably higher for ![]() $O(Re^2)$.
$O(Re^2)$.
Table 1. A direct comparison of the quantitative increase of ![]() $U$ at
$U$ at ![]() $O(Re)$ and
$O(Re)$ and ![]() $O(Re^2)$.
$O(Re^2)$.

6. Conclusions
In this work we have demonstrated the role of convective inertial forces of the external fluid medium on the self-propulsion of a viscous droplet with an inhomogeneous interfacial tension. We consider a generic axisymmetric framework for the inhomogeneous surface tension, and determine the exact analytical solution of the interior and exterior streamfunctions up to first (![]() $O(Re)$) and an approximated second (
$O(Re)$) and an approximated second (![]() $O(Re^2)$) order solution in Reynolds number by utilizing the singular perturbation and matched asymptotic solution technique.
$O(Re^2)$) order solution in Reynolds number by utilizing the singular perturbation and matched asymptotic solution technique.
The discussion shows that, in the present model, the singular perturbation technique yields accurate migration velocity for the droplet under the assertion of low Reynolds number (![]() $Re<1$) and viscosity ratio (
$Re<1$) and viscosity ratio (![]() $\lambda <1$) limits both at
$\lambda <1$) limits both at ![]() $O(Re)$ and
$O(Re)$ and ![]() $O(Re^2)$. It may be noted that the stress parameter
$O(Re^2)$. It may be noted that the stress parameter ![]() $\sigma$ which is the ratio of the amplitudes of the first two modes of the stress field induced by the variable interfacial tension is comparable to
$\sigma$ which is the ratio of the amplitudes of the first two modes of the stress field induced by the variable interfacial tension is comparable to ![]() $\beta$ for the solid squirmers. This distinguishes the swimming features of the active droplet and acts as a decisive parameter in governing the swimming characteristics of the droplet at finite
$\beta$ for the solid squirmers. This distinguishes the swimming features of the active droplet and acts as a decisive parameter in governing the swimming characteristics of the droplet at finite ![]() $Re$.
$Re$.
In contrast to the solid squirmers, where the effect of inertia increases the speed of a pusher (![]() $\beta <0$) swimmer and decreases the speed of a puller (
$\beta <0$) swimmer and decreases the speed of a puller (![]() $\beta >0$), in the case of swimming droplets the foreseen antisymmetry is broken. The finite inertial effect of the surrounding medium enables a systematic increase in the locomotion speed and swimming efficiency of the droplet for all
$\beta >0$), in the case of swimming droplets the foreseen antisymmetry is broken. The finite inertial effect of the surrounding medium enables a systematic increase in the locomotion speed and swimming efficiency of the droplet for all ![]() $\sigma$ values. As was to be expected, at
$\sigma$ values. As was to be expected, at ![]() $O(Re^2)$, due to the quadratic coupling with the Reynolds number, the migration velocity exhibits a substantial increase for both
$O(Re^2)$, due to the quadratic coupling with the Reynolds number, the migration velocity exhibits a substantial increase for both ![]() $\sigma >0$ or
$\sigma >0$ or ![]() $\sigma <0$ compared to
$\sigma <0$ compared to ![]() $O(Re)$. However, the difference between
$O(Re)$. However, the difference between ![]() $\sigma >0$ or
$\sigma >0$ or ![]() $\sigma <0$ can be understood by considering how inertia perturbs the corresponding flow fields and is perceivable in the augmentation of the migration velocity.
$\sigma <0$ can be understood by considering how inertia perturbs the corresponding flow fields and is perceivable in the augmentation of the migration velocity.
Typically, a droplet with ![]() $\sigma <0$ is ineffective than its compliments due to its distinct swimming style. In this particular case, the stresslets generated by the droplet in the exterior medium intensify and the associated surface stress in the direction of migration increases at finite
$\sigma <0$ is ineffective than its compliments due to its distinct swimming style. In this particular case, the stresslets generated by the droplet in the exterior medium intensify and the associated surface stress in the direction of migration increases at finite ![]() $Re$. This disadvantage is partially prevailed over by the presence of the counter-rotating vortices of the interior fluid towards the direction of migration. Interestingly, for
$Re$. This disadvantage is partially prevailed over by the presence of the counter-rotating vortices of the interior fluid towards the direction of migration. Interestingly, for ![]() $\sigma <0$, we identify that due to extended stresslets, the apparent extent of the swimmer increases at finite
$\sigma <0$, we identify that due to extended stresslets, the apparent extent of the swimmer increases at finite ![]() $Re$. This prompts an interplay among the inertial effect of the surrounding medium and the viscosity ratio of the droplet at higher
$Re$. This prompts an interplay among the inertial effect of the surrounding medium and the viscosity ratio of the droplet at higher ![]() $\lambda$ (in the limit
$\lambda$ (in the limit ![]() $\lambda <1$), and subsequently the viscous power dissipation and the swimming efficiency differs from the monotonically decreasing and increasing Stokesian behaviour, respectively. Our findings also provide insights into an alternative illustration of the effect of inertia by visualizing the nonlinear drag function of the droplet in the phase space of the migration velocity. The linear stability analysis of the associated drag function at
$\lambda <1$), and subsequently the viscous power dissipation and the swimming efficiency differs from the monotonically decreasing and increasing Stokesian behaviour, respectively. Our findings also provide insights into an alternative illustration of the effect of inertia by visualizing the nonlinear drag function of the droplet in the phase space of the migration velocity. The linear stability analysis of the associated drag function at ![]() $O(Re)$ is to identify an asymptotically stable non-zero migration state for the droplet, which solely occurs due to the convective inertial forcing of the surrounding medium.
$O(Re)$ is to identify an asymptotically stable non-zero migration state for the droplet, which solely occurs due to the convective inertial forcing of the surrounding medium.
In summary, our approach is not restricted to a particular choice of external source that induces a variability in the surface tension, thus the above results can be applied to broader class of active droplets. Although the behaviours are manifested at the low viscosity ratio limit, the present framework probe deeper insights into the migration of a single swimming droplet at finite ![]() $Re$. The present results scale the migration velocity and relevant swimming characteristics of the droplet with the corresponding size and enhance the ability of the droplet to operate at higher flow rates. These are significant advantages for separation and filtration applications in micro-fluidic systems (Di Carlo Reference Di Carlo2009; Martel & Toner Reference Martel and Toner2014), and will stimulate experimental studies on artificial swimmers incorporating the inertial effect.
$Re$. The present results scale the migration velocity and relevant swimming characteristics of the droplet with the corresponding size and enhance the ability of the droplet to operate at higher flow rates. These are significant advantages for separation and filtration applications in micro-fluidic systems (Di Carlo Reference Di Carlo2009; Martel & Toner Reference Martel and Toner2014), and will stimulate experimental studies on artificial swimmers incorporating the inertial effect.
Acknowledgements
The second and third authors acknowledge the financial support from SERB, Government of India, project wide EMR/2016/000879. The authors report no conflict of interests.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Solution of streamfunction in the Oseen regime
On employing the Goldstein transformation (Goldstein Reference Goldstein1929), the leading-order contribution of ![]() $E_{\hat {r}}^{2} \varPsi _{1}^{e}$ which necessarily satisfies
$E_{\hat {r}}^{2} \varPsi _{1}^{e}$ which necessarily satisfies ![]() $Re E_{\hat {r}}^{2}\varPsi _{1}^{e} \sim O(1)$ in the stokes regime, can be written as (Proudman & Pearson Reference Proudman and Pearson1957; Khair & Chisholm Reference Khair and Chisholm2011)
$Re E_{\hat {r}}^{2}\varPsi _{1}^{e} \sim O(1)$ in the stokes regime, can be written as (Proudman & Pearson Reference Proudman and Pearson1957; Khair & Chisholm Reference Khair and Chisholm2011)
 \begin{align} E_{\hat{r}}^{2}\varPsi_{1}^{e} & = \textrm{e}^{\hat{r}\eta/2}\, ({\rm \pi}/2)^{1/2} \textrm{e}^{-{\hat{r}}/{2}} \left( 1+ \frac{2}{\hat{r}} \right) \, \mathcal{A}_1 \, Q_{1}(\eta) \nonumber\\ & = \exp\left({-\frac{\hat{r}}{2} (1- \eta)}\right) \,({\rm \pi}/2)^{1/2} \left( 1+ \frac{2}{\hat{r}} \right) \, \mathcal{A}_1 \, Q_{1}(\eta). \end{align}
\begin{align} E_{\hat{r}}^{2}\varPsi_{1}^{e} & = \textrm{e}^{\hat{r}\eta/2}\, ({\rm \pi}/2)^{1/2} \textrm{e}^{-{\hat{r}}/{2}} \left( 1+ \frac{2}{\hat{r}} \right) \, \mathcal{A}_1 \, Q_{1}(\eta) \nonumber\\ & = \exp\left({-\frac{\hat{r}}{2} (1- \eta)}\right) \,({\rm \pi}/2)^{1/2} \left( 1+ \frac{2}{\hat{r}} \right) \, \mathcal{A}_1 \, Q_{1}(\eta). \end{align}
The vorticity (![]() $\sim E^2 \psi ^e$) generated by the swimmer in the inner regime primarily gets transported to the corresponding higher order in the Oseen regime (Khair & Chisholm Reference Khair and Chisholm2011). Subsequently, from the leading-order solution (
$\sim E^2 \psi ^e$) generated by the swimmer in the inner regime primarily gets transported to the corresponding higher order in the Oseen regime (Khair & Chisholm Reference Khair and Chisholm2011). Subsequently, from the leading-order solution (![]() $\psi _{0}^{e}$) in the Stokes or inner regime, the associated contribution at
$\psi _{0}^{e}$) in the Stokes or inner regime, the associated contribution at ![]() $O(Re)$ is given by
$O(Re)$ is given by ![]() $E_{r}^{2}\psi _{0}^{e}= (({-2 B_{1}^{e}})/{r})\, Q_{1}$. This leads to
$E_{r}^{2}\psi _{0}^{e}= (({-2 B_{1}^{e}})/{r})\, Q_{1}$. This leads to ![]() $\mathcal {A}_1 \sim - B_{1}^{e}$. Consequently, from the results of Proudman & Pearson (Reference Proudman and Pearson1957), the solution of
$\mathcal {A}_1 \sim - B_{1}^{e}$. Consequently, from the results of Proudman & Pearson (Reference Proudman and Pearson1957), the solution of ![]() $\varPsi _{1}^{e}$ can be written as,
$\varPsi _{1}^{e}$ can be written as,