Article contents
The hydrodynamics of an active squirming particle inside of a porous container
Published online by Cambridge University Press: 28 May 2021
Abstract
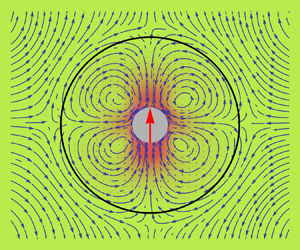
A microswimmer placed inside of a passive lamellar vesicle can hydrodynamically induce directed motion of the vesicle so long as fluid is permitted to pass through the vesicle's surface. With an interest in understanding the underlying theoretical mechanism responsible for this directed motion, we study the low Reynolds number fluid mechanics of a reduced system in which a spherical squirming particle is encapsulated inside of a rigid porous spherical container (membrane). We create a theoretical model for this system and obtain two exact analytical solutions to the Stokes equations which describe the motion of the squirmer and container under porous and non-porous container descriptions. Fluid flow through the container's surface is described using a model similar to Darcy's law where proportionality constants,  $R_{\parallel }$ and
$R_{\parallel }$ and  $R_{\perp }$, parameterize the container's resistance to permeable flow parallel and normal to the container's surface. We numerically simulate trajectories of the squirmer–container system by reformulating the fluid mechanics problem as a coupled set of second kind boundary integral equations (BIEs). This system of BIEs is solved numerically using a Galerkin boundary element discretization on graphics processing units enabled with NVIDIA's Compute Unified Device Architecture. We obtain excellent agreement between the analytical and numerical solutions for the concentric geometry. Trajectories of pusher squirmers show earlier radial spread towards the container's surface, whereas puller squirmers tend to move radially inwards, towards the container's centre. Both the squirmer type (pusher, puller, neutral) and container resistance parameters heavily influence net container motion and early squirmer dynamics.
$R_{\perp }$, parameterize the container's resistance to permeable flow parallel and normal to the container's surface. We numerically simulate trajectories of the squirmer–container system by reformulating the fluid mechanics problem as a coupled set of second kind boundary integral equations (BIEs). This system of BIEs is solved numerically using a Galerkin boundary element discretization on graphics processing units enabled with NVIDIA's Compute Unified Device Architecture. We obtain excellent agreement between the analytical and numerical solutions for the concentric geometry. Trajectories of pusher squirmers show earlier radial spread towards the container's surface, whereas puller squirmers tend to move radially inwards, towards the container's centre. Both the squirmer type (pusher, puller, neutral) and container resistance parameters heavily influence net container motion and early squirmer dynamics.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


