Article contents
Hydrodynamic interactions among multiple circular cylinders in an inviscid flow
Published online by Cambridge University Press: 09 October 2012
Abstract
Hydrodynamic interactions among multiple circular cylinders translating in an otherwise undisturbed inviscid fluid are theoretically investigated. A constructive method for solving a Neumann boundary-value problem in a domain outside  $N$ circles (one kind of Hilbert boundary-value problem in the complex plane) is presented in the study to derive the velocity potential of the liquid. The method employs successive offset functions combined with a ‘generalized cyclic permutation’ in turn to satisfy the impenetrable boundary condition on each circle. The complex potential is therefore expressed as
$N$ circles (one kind of Hilbert boundary-value problem in the complex plane) is presented in the study to derive the velocity potential of the liquid. The method employs successive offset functions combined with a ‘generalized cyclic permutation’ in turn to satisfy the impenetrable boundary condition on each circle. The complex potential is therefore expressed as 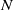 $N$ isolated singularities in power series form and used to get instantaneous added masses of
$N$ isolated singularities in power series form and used to get instantaneous added masses of 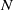 $N$ submerged circular cylinders. Then, based on the Hamilton variational principle, a dynamical equation of motion in vector form is derived to predict nonlinear translations of the submerged bodies under fully hydrodynamic interactions. Also, the equivalence of the energy-based Lagrangian framework and a momentum-type one in the two-dimensional body–liquid system is proved. It implies that the pressure integration around a submerged body is holographic, which provides information about velocities and accelerations of all bodies. The numerical solutions indicate some typical dynamical behaviours of more than two circular cylinders which reveal that interesting nonlinear phenomena would appear in such a system with simple physical assumptions.
$N$ submerged circular cylinders. Then, based on the Hamilton variational principle, a dynamical equation of motion in vector form is derived to predict nonlinear translations of the submerged bodies under fully hydrodynamic interactions. Also, the equivalence of the energy-based Lagrangian framework and a momentum-type one in the two-dimensional body–liquid system is proved. It implies that the pressure integration around a submerged body is holographic, which provides information about velocities and accelerations of all bodies. The numerical solutions indicate some typical dynamical behaviours of more than two circular cylinders which reveal that interesting nonlinear phenomena would appear in such a system with simple physical assumptions.
Information
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 2
- Cited by

