Article contents
A hybrid artificial intelligence control of a turbulent jet: Reynolds number effect and scaling
Published online by Cambridge University Press: 27 May 2022
Abstract
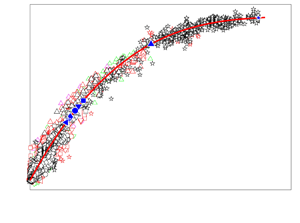
This work aims to investigate experimentally the effect of the Reynolds number Re, based on the nozzle diameter D, on jet mixing manipulation using an unsteady radial minijet. A novel artificial intelligence (AI) control system has been developed to manipulate the jet over Re = 5800–40 000. The system may optimize simultaneously the control law and a time-independent parameter, which dictate the actuation ON/OFF states and amplitude, respectively. The control parameters include the mass flow rate, excitation frequency and diameter ratios (Cm, fe/f0 and d/D) of the minijet to the main jet as well as the duty cycle (α) of minijet injection. Jet mixing is quantified using Ke and K0, where K is the decay rate of the jet centreline mean velocity, and subscripts e and 0 denote the manipulated and unforced jets, respectively. It has been found that the maximum Ke achievable does not vary with Re. Scaling analysis of the huge volume of experimental data obtained from the AI system reveals that the relationship Ke = g1 (Cm, fe/f0, α, d/D, Re, K0) may be reduced to Ke/K0 = g2  $(\zeta )$, where g1 and g2 are different functions and the scaling factor
$(\zeta )$, where g1 and g2 are different functions and the scaling factor  $\zeta = ({C_m}/\alpha ){(D/d)^{1 - n}}(1/Re){({f_e}/{f_{e,opt}})^m}$, m and 1 − n are the power indices, and subscript opt denotes the value at which Ke is maximum. The scaling law is discussed in detail, along with the physical meanings of the dimensionless parameters Ke/K0, ζ,
$\zeta = ({C_m}/\alpha ){(D/d)^{1 - n}}(1/Re){({f_e}/{f_{e,opt}})^m}$, m and 1 − n are the power indices, and subscript opt denotes the value at which Ke is maximum. The scaling law is discussed in detail, along with the physical meanings of the dimensionless parameters Ke/K0, ζ,  $({C_m}/\alpha ){(D/d)^{1 - n}}(1/Re)$ and
$({C_m}/\alpha ){(D/d)^{1 - n}}(1/Re)$ and  ${({f_e}/{f_{e,opt}})^m}$.
${({f_e}/{f_{e,opt}})^m}$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Joint first authors.
References
- 7
- Cited by


