Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T06:09:39.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Horizontal turbulent diffusion in a convective mixed layer

Published online by Cambridge University Press:  10 October 2014

Junshi Ito ,
Hiroshi Niino  and
Mikio Nakanishi
Junshi Ito*
Affiliation:
Atmosphere and Ocean Research Institute, The University of Tokyo, Kashiwa, Chiba, 277-8564, Japan
Hiroshi Niino
Affiliation:
Atmosphere and Ocean Research Institute, The University of Tokyo, Kashiwa, Chiba, 277-8564, Japan
Mikio Nakanishi
Affiliation:
National Defense Academy, Yokosuka, Kanagawa, 239-0811, Japan
*
†Email address for correspondence: junshi@aori.u-tokyo.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

A large eddy simulation (LES) is used to estimate a reliable horizontal turbulent diffusion coefficient, 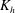$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K_{{h}}$ , in a convective mixed layer (CML). The introduction of a passive scalar field with a fixed horizontal gradient at a given time enables 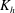$K_{{h}}$ estimation as a function of height, based on the simulated turbulent horizontal scalar flux. Here 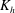$K_{{h}}$ is found to be of the order of 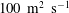$100\ {\mathrm{m}}^2\ {\mathrm{s}}^{-1}$ for a typical terrestrial atmospheric CML. It is shown to scale by the product of the CML convective velocity, 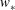$w_{*}$ , and its depth, 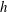$h$ . Here 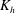$K_{{h}}$ is characterized by a vertical profile in the CML: it is large near both the bottom and top of the CML, where horizontal flows associated with convection are large. The equation pertaining to the temporal rate of change of a horizontal scalar flux suggests that 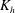$K_{{h}}$ is determined by a balance between production and pressure correlation at a fully developed stage. Pressure correlation near the bottom of the CML is localized in convergence zones near the boundaries of convective cells and becomes large within an eddy turnover time, 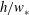$h/w_{*}$ , after the introduction of the passive scalar field.

JFM classification

Convection: Buoyant boundary layers

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 553 - 564
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Briggs, G. A. 1993 Plume dispersion in the convective boundary layer. Part II: analyses of CONDORS field experiment data. J. Appl. Meteorol. 32, 1388–1425.Google Scholar
Byun, D. & Schere, K. L. 2006 Review of the governing equations, computational algorithms, and other components of the models: 3. Community Multiscale Air Quality (CMAQ) modeling system. Appl. Mech. Rev. 59, 51–77.CrossRefGoogle Scholar
Chino, M. & Ishikawa, H. 1988 Experimental verification study for system for prediction of environmental emergency dose information: SPEEDI, (ii). J. Nucl. Sci. Technol. 25, 805–815.CrossRefGoogle Scholar
Deardorff, J. W. 1970 Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27, 1211–1213.Google Scholar
Degrazia, G. A., Rizza, U., Mangia, C. & Tirabassi, T. 1997 Validation of a new turbulent parameterization for dispersion models in convective conditions. Boundary-Layer Meteorol. 85, 243–254.Google Scholar
Dosio, A., Guerau de Arellano, J. V., Holtslag, A. A. M. & Builtjes, P. J. H. 2005 Relating Eulerian and Lagrangian statistics for the turbulent dispersion in the atmospheric convective boundary layer. J. Atmos. Sci. 62, 1175–1191.CrossRefGoogle Scholar
Eberhard, W. L., Moninger, W. R. & Briggs, G. A. 1988 Plume dispersion in the convective boundary layer. Part I: CONDORS field experiment and example measurements. J. Appl. Meteorol. 27, 599–616.Google Scholar
Fedorovich, E., Conzemius, R., Esau, I., Chow, F. K., Lewellen, D., Moeng, C.-H., Sullivan, P., Pino, D. & de Arellano, J.-G.2004 Entrainment into sheared convective boundary layers as predicted by different large eddy simulation codes. In 16th Symposium on Boundary Layers and Turbulence.Google Scholar
Gifford, F. A. 1961 Use of routine meteorological observations for estimating atmospheric dispersion. Nucl. Safety 2, 47–51.Google Scholar
Gifford, F. A. 1982 Horizontal diffusion in the atmosphere: a Lagrangian-dynamical theory. Atmos. Environ. 16, 505–512.Google Scholar
Hong, S. Y. & Pan, H. L. 1996 Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weath. Rev. 124, 2322–2339.Google Scholar
Hotta, H., Iida, Y. & Yokoyama, T. 2012 Estimation of turbulent diffusivity with direct numerical simulation of stellar convection. Astrophys. J. Lett. 751, L9.Google Scholar
Ito, J., Niino, H. & Nakanishi, M. 2010a Large eddy simulation of dust devils in a diurnally-evolving convective mixed layer. J. Met. Soc. Japan 88, 64–77.CrossRefGoogle Scholar
Ito, J., Niino, H. & Nakanishi, M. 2010b Large eddy simulation on dust suspension in a convective mixed layer. SOLA 6, 133–136.Google Scholar
Mellor, G. L. & Yamada, T. 1974 A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 31, 1791–1806.Google Scholar
Mironov, D. V. 2009 Turbulence in the lower troposphere: second-order closure and mass-flux modelling frameworks. In Interdisciplinary Aspects of Turbulence, Lecture Notes in Physics, vol. 756, pp. 1–61. Springer.Google Scholar
Morino, Y., Ohara, T. & Nishizawa, M. 2011 Atmospheric behavior, deposition, and budget of radioactive materials from the Fukushima Daiichi nuclear power plant in March 2011. Geophys. Res. Lett. 38, L00G11.Google Scholar
Nakanishi, M. & Niino, H. 2009 Development of an improved turbulence closure model for the atmospheric boundary layer. J. Met. Soc. Japan 87, 895–912.Google Scholar
Panofsky, H. A. & Dutton, J. A. 1983 Atmospheric Turbulence. Wiley-Interscience.Google Scholar
Plate, E. J., Fedorovich, E. E., Viegas, D. X. & Wyngaard, J. C. 1998 Buoyant Convection in Geophysical Flows. Kluwer Academic.Google Scholar
Schmidt, H. & Schumann, U. 1989 Coherent structure of the convective boundary layer derived from large-eddy simulations. J. Fluid Mech. 200, 511–562.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. 1. The basic experiment. Mon. Weather Rev. 91, 99–164.Google Scholar
Terada, H., Nagai, H. & Yamazawa, H. 2013 Validation of a Lagrangian atmospheric dispersion model against middle-range scale measurements of 85Kr concentration in Japan. J. Nucl. Sci. Technol. 50, 1198–1212.Google Scholar
Weil, J. C., Sullivan, P., Patton, E. & Moeng, C.-H. 2012 Statistical variability of dispersion in the convective boundary layer: ensembles of simulations and observations. Boundary-Layer Meteorol. 145, 185–210.Google Scholar
Willis, G. E. & Deardorff, J. W. 1981 A laboratory study of dispersion from a source in the middle of the convectively mixed layer. Atmos. Environ. 15, 109–117.Google Scholar