Article contents
High-speed boundary-layer transition induced by a discrete roughness element
Published online by Cambridge University Press: 24 July 2013
Abstract
Direct numerical simulation (DNS) is used to study laminar to turbulent transition induced by a discrete hemispherical roughness element in a high-speed laminar boundary layer. The simulations are performed under conditions matching the experiments of Danehy et al. (AIAA Paper 2009–394, 2009) for free-stream Mach numbers of 3.37, 5.26 and 8.23. It is observed that the Mach 8.23 flow remains laminar downstream of the roughness, while the lower Mach numbers undergo transition. The Mach 3.37 flow undergoes transition closer to the bump when compared with Mach 5.26, in agreement with experimental observations. Transition is accompanied by an increase in 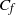 ${C}_{f} $ and
${C}_{f} $ and 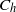 ${C}_{h} $ (Stanton number). Even for the case that did not undergo transition (Mach 8.23), streamwise vortices induced by the roughness cause a significant rise in
${C}_{h} $ (Stanton number). Even for the case that did not undergo transition (Mach 8.23), streamwise vortices induced by the roughness cause a significant rise in 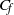 ${C}_{f} $ until 20
${C}_{f} $ until 20 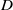 $D$ downstream. The mean van Driest transformed velocity and Reynolds stress for Mach 3.37 and 5.26 show good agreement with available data. Temporal spectra of pressure for Mach 3.37 show that frequencies in the range of 10–1000 kHz are dominant. The transition process involves the following key elements: upon interaction with the roughness element, the boundary layer separates to form a series of spanwise vortices upstream of the roughness and a separation shear layer. The system of spanwise vortices wrap around the roughness element in the form of horseshoe/necklace vortices to yield a system of counter-rotating streamwise vortices downstream of the element. These vortices are located beneath the separation shear layer and perturb it, which results in the formation of trains of hairpin-shaped vortices further downstream of the roughness for the cases that undergo transition. These hairpins spread in the span with increasing downstream distance and the flow increasingly resembles a fully developed turbulent boundary layer. A local Reynolds number based on the wall properties is seen to correlate with the onset of transition for the cases considered.
$D$ downstream. The mean van Driest transformed velocity and Reynolds stress for Mach 3.37 and 5.26 show good agreement with available data. Temporal spectra of pressure for Mach 3.37 show that frequencies in the range of 10–1000 kHz are dominant. The transition process involves the following key elements: upon interaction with the roughness element, the boundary layer separates to form a series of spanwise vortices upstream of the roughness and a separation shear layer. The system of spanwise vortices wrap around the roughness element in the form of horseshoe/necklace vortices to yield a system of counter-rotating streamwise vortices downstream of the element. These vortices are located beneath the separation shear layer and perturb it, which results in the formation of trains of hairpin-shaped vortices further downstream of the roughness for the cases that undergo transition. These hairpins spread in the span with increasing downstream distance and the flow increasingly resembles a fully developed turbulent boundary layer. A local Reynolds number based on the wall properties is seen to correlate with the onset of transition for the cases considered.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 46
- Cited by

