Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-25T19:32:25.237Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transport modification by finitely extensible polymers in laminar boundary layer flow

Published online by Cambridge University Press:  07 January 2016

Roberto Benzi ,
Emily S. C. Ching ,
Wilson C. K. Yu  and
Yiqu Wang
Roberto Benzi
Affiliation:
Dip. di Fisica and INFN, Università ‘Tor Vergata’, Via della Ricerca Scientifica 1, I-00133 Roma, Italy
Emily S. C. Ching*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong Institute of Theoretical Physics, The Chinese University of Hong Kong, Shatin, Hong Kong
Wilson C. K. Yu
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong
Yiqu Wang
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong
*
†Email address for correspondence: ching@phy.cuhk.edu.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

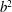We study how heat transport is affected by finitely extensible polymers in a laminar boundary layer flow within the framework of the Prandtl–Blasius–Pohlhausen theory. The polymers are described by the finitely extensible nonlinear elastic-Peterlin model with a parameter $b^{2}$, which is the ratio of the maximum to the equilibrium value of the trace of the polymer conformation tensor. For very large 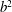$b^{2}$, heat transport is reduced. When 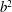$b^{2}$ is small, heat transport is enhanced. We investigate the transition from heat reduction to heat enhancement as a function of the polymer relaxation time and concentration, and show that the transition can be explained in terms of the functional shape of the space-dependent effective viscosity due to the polymers.

JFM classification

Boundary Layers: Boundary Layers Non-Newtonian Flows: Non-Newtonian Flows Non-Newtonian Flows: Polymers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 337 - 357
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Acrivos, A., Shah, M. J. & Petersen, E. E. 1960 Momentum and heat transfer in laminar boundary-layer flows of non-Newtonian fluids past external surfaces. AIChE J. 6, 312–317.Google Scholar
Ahlers, G., Brown, E., Fontenele, A., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Ahlers, G. & Nikolaenko, A. 2010 Effect of a polymer additive on heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 034503.Google Scholar
Bataller, R. C. 2008 Similarity solutions for boundary layer flow and heat transfer of a FENE-P fluid with thermal radiation. Phys. Lett. A 372, 2431–2439.Google Scholar
Benzi, R., Ching, E. S. C. & Chu, V. W. S. 2012 Heat transport by laminar boundary layer flow with polymers. J. Fluid Mech. 696, 330–344.Google Scholar
Benzi, R., Ching, E. S. C. & De Angelis, E. 2010 Effect of polymer additives on heat transport in turbulent thermal convection. Phys. Rev. Lett. 104, 024502.Google Scholar
Bird, R. B., Hassager, O., Armstrong, R. C. & Curtis, C. F. 1987 Dynamics of Polymeric Liquids. Wiley-Interscience.Google Scholar
Cebeci, T. 2002 Convective Heat Transfer. Springer.Google Scholar
Delouei, A. A., Nazari, M., Kayhani, M. H. & Succi, S. 2014 Non-Newtonian unconfined flow and heat transfer over a heated cylinder using the direct-forcing immersed boundary thermal lattice Boltzmann method. Phys. Rev. E 89, 053312.Google Scholar
Dubief, Y.2010 Heat transfer enhancement and reduction by poylmer additives in turbulent Rayleigh–Bénard convection. arXiv:1009.0493v1.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.Google Scholar
James, D. F. & Acosta, A. J. 1970 The laminar flow of dilute polymer solutions around circular cylinders. J. Fluid Mech. 42, 269–288.Google Scholar
Khan, W. A., Culham, J. R. & Yovanovich, M. M. 2006 Fluid flow and heat transfer in power-law fluids across circular cylinders: analytical study. Trans. ASME J. Heat Transfer 128, 870–878.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Min, T., Yoo, J. Y., Choi, H. & Joseph, D. D. 2003 Drag reduction by polymer additives in a turbulent channel flow. J. Fluid Mech. 486, 213–238.Google Scholar
Mizushina, T., Usui, H., Veno, K. & Kato, T. 1978 Experiments of pseudoplastic fluid cross flow around a circular cylinder. Heat Transfer Japan. Res. 7, 92101.Google Scholar
Olagunju, D. O. 2006 A self-similar solution for forced convection boundary layer flow of a FENE-P fluid. Appl. Maths Lett. 19, 432–436.Google Scholar
Schlichting, H. & Gersten, K. 2004 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.Google Scholar
Toms, B. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. Intl Rheol. Congr. 2, 135–141.Google Scholar
Wei, P., Ni, R. & Xia, K.-Q. 2012 Enhanced and reduced heat transport in turbulent thermal convection with polymer additives. Phys. Rev. E 86, 016325.Google Scholar