Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhou, Jiayi
and
Andersson, Mats
2020.
An analysis of surface breakup induced by laser-generated cavitation bubbles in a turbulent liquid jet.
Experiments in Fluids,
Vol. 61,
Issue. 12,
Chung, Jaeho
Seo, Yonghyun
and
Shin, Young S.
2020.
Dynamic and whipping response of the surface ship subjected to underwater explosion: experiment and simulation.
Ships and Offshore Structures,
Vol. 15,
Issue. 10,
p.
1129.
Huang, Guohao
Zhang, Mindi
Ma, Xiaojian
Chang, Qing
Zheng, Chen
and
Huang, Biao
2020.
Dynamic behavior of a single bubble between the free surface and rigid wall.
Ultrasonics Sonochemistry,
Vol. 67,
Issue. ,
p.
105147.
Liu, Wei
Li, Ning
Huang, Xiao-long
Kang, Yang
Li, Can
Qiang, Wei
and
Weng, Chun-sheng
2021.
Experimental study of underwater pulse detonation gas jets: Bubble velocity field and time–frequency characteristics of pressure field.
Physics of Fluids,
Vol. 33,
Issue. 8,
Li, Shi-Min
Liu, Yun-Long
Wang, Qianxi
and
Zhang, A-Man
2021.
Dynamics of a buoyant pulsating bubble near two crossed walls.
Physics of Fluids,
Vol. 33,
Issue. 7,
Bempedelis, N.
Zhou, J.
Andersson, M.
and
Ventikos, Y.
2021.
Numerical and experimental investigation into the dynamics of a bubble-free-surface system.
Physical Review Fluids,
Vol. 6,
Issue. 1,
Basak, Saswata
Farsoiya, Palas Kumar
and
Dasgupta, Ratul
2021.
Jetting in finite-amplitude, free, capillary-gravity waves.
Journal of Fluid Mechanics,
Vol. 909,
Issue. ,
Han, Rui
Zhang, A-Man
Tan, Sichao
and
Li, Shuai
2022.
Interaction of cavitation bubbles with the interface of two immiscible fluids on multiple time scales.
Journal of Fluid Mechanics,
Vol. 932,
Issue. ,
Deka, Amitjyoti
Baruah, Prahlad K.
Khare, Alika
and
Nath, Arpita
2022.
Inquest of material dissipation from cavitation bubble in laser-irradiated solid–liquid interface.
Radiation Effects and Defects in Solids,
Vol. 177,
Issue. 3-4,
p.
244.
Kayal, Lohit
Basak, Saswata
and
Dasgupta, Ratul
2022.
Dimples, jets and self-similarity in nonlinear capillary waves.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Zhang, Yuning
Zhang, Xiaofei
Zhang, Shurui
Ying, Jiaze
Yang, Yihao
Wang, Hongbo
Li, Zhaohao
and
Zhang, Yuning
2023.
A Review of the Dynamics Progress of Bubble Collapse within Droplet and Droplet Splash.
Applied Sciences,
Vol. 13,
Issue. 13,
p.
7822.
Zhang, Yuning
Zhang, Xiaofei
Zhang, Shurui
Wang, Hongbo
Zha, Kehui
Li, Zhaohao
and
Zhang, Yuning
2023.
Research on Dynamic Process and Droplet Splash of Laser-Induced Cavitation Bubble Collapse within a Droplet.
Applied Sciences,
Vol. 13,
Issue. 13,
p.
7862.
Li, Shuai
Zhao, Zhesheng
Zhang, A-Man
and
Han, Rui
2024.
Cavitation bubble dynamics inside a droplet suspended in a different host fluid.
Journal of Fluid Mechanics,
Vol. 979,
Issue. ,
Zhong, Yuying
Zhao, Yang
Gao, Xiaoyan
and
Bao, Fubing
2024.
Experimental study on interaction between a cavitation bubble and an oil layer–water interface.
AIP Advances,
Vol. 14,
Issue. 6,
Liu, Yang
Zheng, Zhi-Ying
He, Zhi-Bo
Zeng, Tian-Bao
Wang, Lu
Cai, Wei-Hua
and
Qi, Hong
2024.
Interactions between cavitation bubbles and free surfaces of non-Newtonian polymer solutions.
Physics of Fluids,
Vol. 36,
Issue. 9,
Zhang, Tianyuan
Zhang, A-Man
Zhang, Sai
Long, Sinan
Han, Rui
Liu, Luoqin
Ohl, Claus-Dieter
and
Li, Shuai
2025.
Free-surface jetting driven by a cavitating vortex ring.
Journal of Fluid Mechanics,
Vol. 1003,
Issue. ,
Luo, Haotian
Guo, Yunji
Xu, Sheng
Wen, Haocheng
Wu, Wangxia
Xiang, Gaoming
and
Wang, Bing
2025.
Characteristics of a laser-induced bubble near the wedge between the gas–liquid interface and solid wall.
Physics of Fluids,
Vol. 37,
Issue. 1,
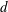 $d$: 0.28–7 mm) below the free surface and the maximum radius of the bubble (
$d$: 0.28–7 mm) below the free surface and the maximum radius of the bubble (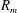 $R_{m}$: 1.5–3.6 mm). When
$R_{m}$: 1.5–3.6 mm). When 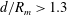 $d/R_{m}>1.3$, the surface wave shows a simple smooth hump (case 1). When
$d/R_{m}>1.3$, the surface wave shows a simple smooth hump (case 1). When 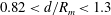 $0.82<d/R_{m}<1.3$, a single droplet or multiple droplets are pinched off sequentially or simultaneously at the tip or from some points of the jet-like surface wave (case 2). Finally, when
$0.82<d/R_{m}<1.3$, a single droplet or multiple droplets are pinched off sequentially or simultaneously at the tip or from some points of the jet-like surface wave (case 2). Finally, when 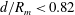 $d/R_{m}<0.82$, a series of squirting and jetting phenomena are observed at the top of the jet-like surface wave (case 3). For case 1, a proportional relationship is found between
$d/R_{m}<0.82$, a series of squirting and jetting phenomena are observed at the top of the jet-like surface wave (case 3). For case 1, a proportional relationship is found between 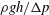 $\unicode[STIX]{x1D70C}gh/\unicode[STIX]{x0394}p$ and
$\unicode[STIX]{x1D70C}gh/\unicode[STIX]{x0394}p$ and 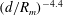 $(d/R_{m})^{-4.4}$, where
$(d/R_{m})^{-4.4}$, where 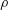 $\unicode[STIX]{x1D70C}$ is the density of the fluid,
$\unicode[STIX]{x1D70C}$ is the density of the fluid, 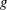 $g$ is the gravitational acceleration and
$g$ is the gravitational acceleration and 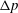 $\unicode[STIX]{x0394}p$ is the difference between the reference atmospheric pressure and the vapour pressure inside a bubble. This proportional relationship is explained semi-analytically using a scaling argument and conservation of momentum and energy, with the help of the Kelvin impulse theory. In addition, we solve the relevant axisymmetric Cauchy–Poisson problem where the initial condition is a jet-like surface wave near its maximum height. By comparing the analytical wave solution with the observed surface wave pattern, it is found that the resultant surface waves are indeed gravity–capillary waves where both the gravity and the surface tension are equally important.
$\unicode[STIX]{x0394}p$ is the difference between the reference atmospheric pressure and the vapour pressure inside a bubble. This proportional relationship is explained semi-analytically using a scaling argument and conservation of momentum and energy, with the help of the Kelvin impulse theory. In addition, we solve the relevant axisymmetric Cauchy–Poisson problem where the initial condition is a jet-like surface wave near its maximum height. By comparing the analytical wave solution with the observed surface wave pattern, it is found that the resultant surface waves are indeed gravity–capillary waves where both the gravity and the surface tension are equally important.