1. Introduction
It is not often in this day and age that physical phenomena commonly observed in nature are explained for the first time in a research article. Yet this is precisely the case when Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) study the fluid dynamics of a familiar sight: ducklings swimming in single file behind their mother. Making the assumption that the rationale for formation swimming is for the ducklings to preserve energy, two questions spring to the fluid dynamicist’s mind: What might the optimal swimming formation be, and how much energy can the ducklings preserve in this way? (Clearly, all considerations here and below apply equally to goslings; only ‘ducklings’ is used for brevity.)
Whether one considers a duck or a supertanker, the physics of the distinctive V-shaped pattern of waves behind it is the same, largely governed by a single non-dimensional group, the Froude number  $Fr = V/\sqrt {gL}$; here,
$Fr = V/\sqrt {gL}$; here,  $V$ is the swimming velocity over water,
$V$ is the swimming velocity over water,  $g$ the gravitational acceleration and
$g$ the gravitational acceleration and  $L$ the length of the submerged surface of the duck from ‘bow’ to ‘stern’. Hence, the system under consideration is highly scalable, from the largest ships down to centimetre scale, where also surface tension effects could become significant. The waves made by a row of ducks is thus an immediate extension of the very system famously considered by Lord Kelvin (Thomson Reference Thomson (Lord Kelvin)1887).
$L$ the length of the submerged surface of the duck from ‘bow’ to ‘stern’. Hence, the system under consideration is highly scalable, from the largest ships down to centimetre scale, where also surface tension effects could become significant. The waves made by a row of ducks is thus an immediate extension of the very system famously considered by Lord Kelvin (Thomson Reference Thomson (Lord Kelvin)1887).
Particular to vessels (in a wide sense) travelling on the water surface, is that a portion of the drag force is due to making waves. In addition to viscous losses, the vessel does work on its surrounding fluid, causing energy to be radiated in the form of waves in its wake. Ducks typically swim at a commendably constant Froude number, a typical value of which Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) estimate at  $Fr\sim 0.25$ for a mother duck. The ducklings’ Froude number will be somewhat higher due to their smaller size, which brings them into the same category as medium-sized vessels such as tugboats and fishing boats (Li, Smeltzer & Ellingsen Reference Li, Smeltzer and Ellingsen2019), for which wave resistance can amount to roughly half the hydrodynamic drag (Faltinsen Reference Faltinsen2005). It is reasonable to focus on the wave resistance when detailed formations are compared; while there is an expected reduction also in viscous drag due to ‘drafting’, well known to cyclists and swimmers as a benefit of moving in the wake of another (Janssen, Wilson & Toussaint Reference Janssen, Wilson and Toussaint2009; Blocken et al. Reference Blocken, Defraeye, Koninkx, Carmeliet and Hespel2013), it is not likely to be highly sensitive to small changes in the exact swimming position.
$Fr\sim 0.25$ for a mother duck. The ducklings’ Froude number will be somewhat higher due to their smaller size, which brings them into the same category as medium-sized vessels such as tugboats and fishing boats (Li, Smeltzer & Ellingsen Reference Li, Smeltzer and Ellingsen2019), for which wave resistance can amount to roughly half the hydrodynamic drag (Faltinsen Reference Faltinsen2005). It is reasonable to focus on the wave resistance when detailed formations are compared; while there is an expected reduction also in viscous drag due to ‘drafting’, well known to cyclists and swimmers as a benefit of moving in the wake of another (Janssen, Wilson & Toussaint Reference Janssen, Wilson and Toussaint2009; Blocken et al. Reference Blocken, Defraeye, Koninkx, Carmeliet and Hespel2013), it is not likely to be highly sensitive to small changes in the exact swimming position.
A remarkable aspect of the work of Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) is that most of their analysis could have been performed many decades ago, had anyone had a mind to do so. The necessary theory goes back a century (Havelock Reference Havelock1919, Reference Havelock1934; Wehausen & Laitone Reference Wehausen and Laitone1960), and numerical methods for this type of set-up (although much developed since) were first implemented a long time ago (e.g. Dawson Reference Dawson1977). Indeed, reducing wave resistance with deliberate destructive interference is the very idea behind the long-since-standard bulbous bow hull design (e.g. Wigley Reference Wigley1936; Kracht Reference Kracht1978). Thus the discoveries of the mechanics of duckling formation which are now presented might seem to some like something of a Columbus’ egg. However, the fact remains that while many might feel they could have analysed the question, Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) were the ones to actually do so, and report it in a clear and illuminating manner.
2. Overview
The premise of Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) is that ducklings swimming behind their mother will organise themselves so that the mother, through the waves she produces, helps the ducklings along. Using classical wave theory, they argue that the single-file formation is favourable and show that, once the ducklings get into a row, two mechanisms allow them to reduce or eliminate their wave resistance, and in some cases even experience a net forward force; Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) term them wave riding and wave passing.
Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) calculate the wave resistance on each duckling, modelled as a semi-submerged ellipsoid, by integrating the anti-streamwise pressure forces acting on its body, obtained using a numerical boundary element method to solve the Laplace equation for ideal flow. For a single duckling, the most favourable position is to ‘ride’ the mother duck's stern wave, somewhat like a surfer uses gravity to propel her down the forward slope of a wave. A duckling riding the wave crest closest behind the mother experiences a wave resistance reduction of more than  $150\,\%$ compared with swimming alone, that is, not only does riding the mother's wave eliminate the wave resistance, but even provides a forward thrust of half the same magnitude.
$150\,\%$ compared with swimming alone, that is, not only does riding the mother's wave eliminate the wave resistance, but even provides a forward thrust of half the same magnitude.
Less intuitive, and all the more striking is the mechanism Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) term wave passing, which occurs when a row of several trailing ducklings is considered. While the first three ducklings in the row can extract some of the mother's radiated wave energy to propel themselves forward, the wave resistance on every additional duckling is also reduced to zero due to a delicate interference which concentrates the waves in a strip directly behind the duckling and eliminates waves radiating outwards to the sides. Some of the wave energy available behind the mother is extracted by the nearest ducklings, and the remainder is passed undiminished along the row until finally radiated in the wake of the last duckling. In the optimal configuration, the ducklings are nearly uniformly spaced separated by one wavelength along line of motion,  $\lambda =2{\rm \pi} V^2/g$.
$\lambda =2{\rm \pi} V^2/g$.
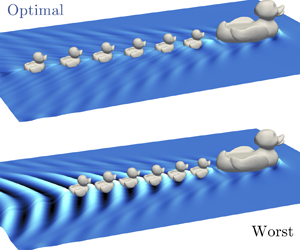
Wave resistance may be calculated either by integrating the pressure forces acting on the duck's body, or through the outward flux of momentum in the wave far field. For a wave-riding duckling the former perspective explains the forward push because the net pressure force has a forward component as the duckling swims ‘downhill’, much like a surfer. The wave-passing phenomenon can perhaps more easily be understood by considering the far field, as shown in figure 1. The waves in a ship's far field is predominantly the sum of those created at the ship's bow and stern, respectively (e.g. Noblesse et al. Reference Noblesse, He, Zhu, Hong, Zhang, Zhu and Yang2014); a ‘wave-passing’ row of ducks thus radiates waves as though it were a single ‘vessel’: the mother's breast is the ‘bow’, the last duckling is the stern, whereas all waves created by the individual ‘bows’ and ‘sterns’ in between are either confined to the near field or eliminated through interference. Remarkably, the wave resistance on the group as a whole thus remains unchanged if more ducklings are added.
Figure 1. The wave-passing phenomenon. (a) Waves created by ducklings in an optimal row configuration can nearly perfectly cancel those from the duckling in front by destructive interference; nearly all waves radiating from the group as a whole originate either from the mother's ‘bow’ or at the ‘stern’ of the last duckling, D6. Each duckling ‘passes’ the stern wave along to the next in line without net energy loss. (b) Drag reduction of each individual compared with swimming alone; drag reduction coefficient  $C_{DR}=100\,\%$ implies zero wave resistance;
$C_{DR}=100\,\%$ implies zero wave resistance;  $C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021).
$C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021).
3. Outlook
Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) convincingly explain one commonly observed swimming formation by demonstrating its potential to considerably economise energy; what remains is to study when and to what extent waterfowl actually do make use of this advantage, perhaps as much a challenge for biologists. An online image search for swimming ducklings quickly indicates that disordered patterns are common, and that also other ordered formations occur. One might say the cost function which the duck family has to minimise is more complicated than energy use alone, including social factors which lie far beyond our expertise as fluid mechanicians.
The benefits of wave riding and wave passing are not exclusive to waterfowl, but could equally apply to boats and vessels at a larger scale. Indeed, it would appear that wave passing, or a highly similar phenomenon, is drawn upon in a recent project, Sea Train, initiated last year by the US Defense Advanced Research Projects Agency (DARPA 2020). Sea Trains are envisioned to consist of four or more unmanned surface vehicles travelling in a row formation. The goal is to ‘utilize surface wave cancellation to minimize the collective wave-making resistance of the Sea Train’, specifically by creating ‘the equivalent of a long parallel mid-body’ (DARPA 2020, p. 5 in HR001120S0010-Amendment-02.pdf). This would seem to describe very well the picture seen in figure 1(a). It could be another example of how some of the best technological solutions are biomimetic, mimicking those already found in nature.

 $C_{DR}=100\,\%$ implies zero wave resistance;
$C_{DR}=100\,\%$ implies zero wave resistance;  $C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (2021).
$C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (2021).


1. Introduction
It is not often in this day and age that physical phenomena commonly observed in nature are explained for the first time in a research article. Yet this is precisely the case when Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) study the fluid dynamics of a familiar sight: ducklings swimming in single file behind their mother. Making the assumption that the rationale for formation swimming is for the ducklings to preserve energy, two questions spring to the fluid dynamicist’s mind: What might the optimal swimming formation be, and how much energy can the ducklings preserve in this way? (Clearly, all considerations here and below apply equally to goslings; only ‘ducklings’ is used for brevity.)
Whether one considers a duck or a supertanker, the physics of the distinctive V-shaped pattern of waves behind it is the same, largely governed by a single non-dimensional group, the Froude number $Fr = V/\sqrt {gL}$; here,
$Fr = V/\sqrt {gL}$; here,  $V$ is the swimming velocity over water,
$V$ is the swimming velocity over water,  $g$ the gravitational acceleration and
$g$ the gravitational acceleration and  $L$ the length of the submerged surface of the duck from ‘bow’ to ‘stern’. Hence, the system under consideration is highly scalable, from the largest ships down to centimetre scale, where also surface tension effects could become significant. The waves made by a row of ducks is thus an immediate extension of the very system famously considered by Lord Kelvin (Thomson Reference Thomson (Lord Kelvin)1887).
$L$ the length of the submerged surface of the duck from ‘bow’ to ‘stern’. Hence, the system under consideration is highly scalable, from the largest ships down to centimetre scale, where also surface tension effects could become significant. The waves made by a row of ducks is thus an immediate extension of the very system famously considered by Lord Kelvin (Thomson Reference Thomson (Lord Kelvin)1887).
Particular to vessels (in a wide sense) travelling on the water surface, is that a portion of the drag force is due to making waves. In addition to viscous losses, the vessel does work on its surrounding fluid, causing energy to be radiated in the form of waves in its wake. Ducks typically swim at a commendably constant Froude number, a typical value of which Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) estimate at $Fr\sim 0.25$ for a mother duck. The ducklings’ Froude number will be somewhat higher due to their smaller size, which brings them into the same category as medium-sized vessels such as tugboats and fishing boats (Li, Smeltzer & Ellingsen Reference Li, Smeltzer and Ellingsen2019), for which wave resistance can amount to roughly half the hydrodynamic drag (Faltinsen Reference Faltinsen2005). It is reasonable to focus on the wave resistance when detailed formations are compared; while there is an expected reduction also in viscous drag due to ‘drafting’, well known to cyclists and swimmers as a benefit of moving in the wake of another (Janssen, Wilson & Toussaint Reference Janssen, Wilson and Toussaint2009; Blocken et al. Reference Blocken, Defraeye, Koninkx, Carmeliet and Hespel2013), it is not likely to be highly sensitive to small changes in the exact swimming position.
$Fr\sim 0.25$ for a mother duck. The ducklings’ Froude number will be somewhat higher due to their smaller size, which brings them into the same category as medium-sized vessels such as tugboats and fishing boats (Li, Smeltzer & Ellingsen Reference Li, Smeltzer and Ellingsen2019), for which wave resistance can amount to roughly half the hydrodynamic drag (Faltinsen Reference Faltinsen2005). It is reasonable to focus on the wave resistance when detailed formations are compared; while there is an expected reduction also in viscous drag due to ‘drafting’, well known to cyclists and swimmers as a benefit of moving in the wake of another (Janssen, Wilson & Toussaint Reference Janssen, Wilson and Toussaint2009; Blocken et al. Reference Blocken, Defraeye, Koninkx, Carmeliet and Hespel2013), it is not likely to be highly sensitive to small changes in the exact swimming position.
A remarkable aspect of the work of Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) is that most of their analysis could have been performed many decades ago, had anyone had a mind to do so. The necessary theory goes back a century (Havelock Reference Havelock1919, Reference Havelock1934; Wehausen & Laitone Reference Wehausen and Laitone1960), and numerical methods for this type of set-up (although much developed since) were first implemented a long time ago (e.g. Dawson Reference Dawson1977). Indeed, reducing wave resistance with deliberate destructive interference is the very idea behind the long-since-standard bulbous bow hull design (e.g. Wigley Reference Wigley1936; Kracht Reference Kracht1978). Thus the discoveries of the mechanics of duckling formation which are now presented might seem to some like something of a Columbus’ egg. However, the fact remains that while many might feel they could have analysed the question, Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) were the ones to actually do so, and report it in a clear and illuminating manner.
2. Overview
The premise of Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) is that ducklings swimming behind their mother will organise themselves so that the mother, through the waves she produces, helps the ducklings along. Using classical wave theory, they argue that the single-file formation is favourable and show that, once the ducklings get into a row, two mechanisms allow them to reduce or eliminate their wave resistance, and in some cases even experience a net forward force; Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) term them wave riding and wave passing.
Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) calculate the wave resistance on each duckling, modelled as a semi-submerged ellipsoid, by integrating the anti-streamwise pressure forces acting on its body, obtained using a numerical boundary element method to solve the Laplace equation for ideal flow. For a single duckling, the most favourable position is to ‘ride’ the mother duck's stern wave, somewhat like a surfer uses gravity to propel her down the forward slope of a wave. A duckling riding the wave crest closest behind the mother experiences a wave resistance reduction of more than $150\,\%$ compared with swimming alone, that is, not only does riding the mother's wave eliminate the wave resistance, but even provides a forward thrust of half the same magnitude.
$150\,\%$ compared with swimming alone, that is, not only does riding the mother's wave eliminate the wave resistance, but even provides a forward thrust of half the same magnitude.
Less intuitive, and all the more striking is the mechanism Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) term wave passing, which occurs when a row of several trailing ducklings is considered. While the first three ducklings in the row can extract some of the mother's radiated wave energy to propel themselves forward, the wave resistance on every additional duckling is also reduced to zero due to a delicate interference which concentrates the waves in a strip directly behind the duckling and eliminates waves radiating outwards to the sides. Some of the wave energy available behind the mother is extracted by the nearest ducklings, and the remainder is passed undiminished along the row until finally radiated in the wake of the last duckling. In the optimal configuration, the ducklings are nearly uniformly spaced separated by one wavelength along line of motion, $\lambda =2{\rm \pi} V^2/g$.
$\lambda =2{\rm \pi} V^2/g$.
Wave resistance may be calculated either by integrating the pressure forces acting on the duck's body, or through the outward flux of momentum in the wave far field. For a wave-riding duckling the former perspective explains the forward push because the net pressure force has a forward component as the duckling swims ‘downhill’, much like a surfer. The wave-passing phenomenon can perhaps more easily be understood by considering the far field, as shown in figure 1. The waves in a ship's far field is predominantly the sum of those created at the ship's bow and stern, respectively (e.g. Noblesse et al. Reference Noblesse, He, Zhu, Hong, Zhang, Zhu and Yang2014); a ‘wave-passing’ row of ducks thus radiates waves as though it were a single ‘vessel’: the mother's breast is the ‘bow’, the last duckling is the stern, whereas all waves created by the individual ‘bows’ and ‘sterns’ in between are either confined to the near field or eliminated through interference. Remarkably, the wave resistance on the group as a whole thus remains unchanged if more ducklings are added.
Figure 1. The wave-passing phenomenon. (a) Waves created by ducklings in an optimal row configuration can nearly perfectly cancel those from the duckling in front by destructive interference; nearly all waves radiating from the group as a whole originate either from the mother's ‘bow’ or at the ‘stern’ of the last duckling, D6. Each duckling ‘passes’ the stern wave along to the next in line without net energy loss. (b) Drag reduction of each individual compared with swimming alone; drag reduction coefficient $C_{DR}=100\,\%$ implies zero wave resistance;
$C_{DR}=100\,\%$ implies zero wave resistance;  $C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021).
$C_{DR}>100\,\%$ means a net forward force. Reproduction of figure 4 from Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021).
3. Outlook
Yuan et al. (Reference Yuan, Chen, Jia, Ji and Incecik2021) convincingly explain one commonly observed swimming formation by demonstrating its potential to considerably economise energy; what remains is to study when and to what extent waterfowl actually do make use of this advantage, perhaps as much a challenge for biologists. An online image search for swimming ducklings quickly indicates that disordered patterns are common, and that also other ordered formations occur. One might say the cost function which the duck family has to minimise is more complicated than energy use alone, including social factors which lie far beyond our expertise as fluid mechanicians.
The benefits of wave riding and wave passing are not exclusive to waterfowl, but could equally apply to boats and vessels at a larger scale. Indeed, it would appear that wave passing, or a highly similar phenomenon, is drawn upon in a recent project, Sea Train, initiated last year by the US Defense Advanced Research Projects Agency (DARPA 2020). Sea Trains are envisioned to consist of four or more unmanned surface vehicles travelling in a row formation. The goal is to ‘utilize surface wave cancellation to minimize the collective wave-making resistance of the Sea Train’, specifically by creating ‘the equivalent of a long parallel mid-body’ (DARPA 2020, p. 5 in HR001120S0010-Amendment-02.pdf). This would seem to describe very well the picture seen in figure 1(a). It could be another example of how some of the best technological solutions are biomimetic, mimicking those already found in nature.
Declaration of interests
The author reports no conflict of interest.