Published online by Cambridge University Press: 01 December 2016
The unsteady response of a water free surface to a localized pressure source moving at constant speed 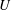 $U$ in the range
$U$ in the range 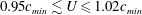 $0.95c_{min}\lesssim U\leqslant 1.02c_{min}$, where
$0.95c_{min}\lesssim U\leqslant 1.02c_{min}$, where 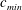 $c_{min}$ is the minimum phase speed of linear gravity–capillary waves in deep water, is investigated through experiments and numerical simulations. This unsteady response state, which consists of a V-shaped pattern behind the source, and features periodic shedding of pairs of depressions from the tips of the V, was first observed qualitatively by Diorio et al. (Phys. Rev. Lett., vol. 103, 2009, 214502) and called state III. In the present investigation, cinematic shadowgraph and refraction-based techniques are utilized to measure the temporal evolution of the free-surface deformation pattern downstream of the source as it moves along a towing tank, while numerical simulations of the model equation described by Cho et al. (J. Fluid Mech., vol. 672, 2011, pp. 288–306) are used to extend the experimental results over longer times than are possible in the experiments. From the experiments, it is found that the speed–amplitude characteristics and the shape of the depressions are nearly the same as those of the freely propagating gravity–capillary lumps of inviscid potential theory. The decay rate of the depressions is measured from their height–time characteristics, which are well fitted by an exponential decay law with an order one decay constant. It is found that the shedding period of the depression pairs decreases with increasing source strength and speed. As the source speed approaches
$c_{min}$ is the minimum phase speed of linear gravity–capillary waves in deep water, is investigated through experiments and numerical simulations. This unsteady response state, which consists of a V-shaped pattern behind the source, and features periodic shedding of pairs of depressions from the tips of the V, was first observed qualitatively by Diorio et al. (Phys. Rev. Lett., vol. 103, 2009, 214502) and called state III. In the present investigation, cinematic shadowgraph and refraction-based techniques are utilized to measure the temporal evolution of the free-surface deformation pattern downstream of the source as it moves along a towing tank, while numerical simulations of the model equation described by Cho et al. (J. Fluid Mech., vol. 672, 2011, pp. 288–306) are used to extend the experimental results over longer times than are possible in the experiments. From the experiments, it is found that the speed–amplitude characteristics and the shape of the depressions are nearly the same as those of the freely propagating gravity–capillary lumps of inviscid potential theory. The decay rate of the depressions is measured from their height–time characteristics, which are well fitted by an exponential decay law with an order one decay constant. It is found that the shedding period of the depression pairs decreases with increasing source strength and speed. As the source speed approaches 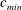 $c_{min}$, this period tends to approximately 1 s for all source magnitudes. At the low-speed boundary of state III, a new response with unsteady asymmetric shedding of depressions is found. This response is also predicted by the model equation.
$c_{min}$, this period tends to approximately 1 s for all source magnitudes. At the low-speed boundary of state III, a new response with unsteady asymmetric shedding of depressions is found. This response is also predicted by the model equation.