Article contents
Friction drag reduction of Taylor–Couette flow over air-filled microgrooves
Published online by Cambridge University Press: 19 November 2024
Abstract
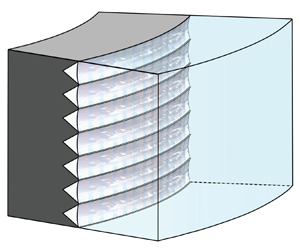
Reducing drag under high turbulence is a critical but challenging issue that has engendered great concern. This study utilizes hydrophilic tips in superhydrophobic (SHP) grooves to enhance the stability of plastron, which results in a considerable drag reduction ( $DR$) up to 62 %, at Reynolds number (
$DR$) up to 62 %, at Reynolds number ( $Re$) reaching
$Re$) reaching  $2.79 \times 10^{4}$. The effect of the spacing width
$2.79 \times 10^{4}$. The effect of the spacing width  $w$ of the microgrooves on both
$w$ of the microgrooves on both  $DR$ and flow structures is investigated. Experimental results demonstrate that
$DR$ and flow structures is investigated. Experimental results demonstrate that  $DR$ increases as either microgroove spacing
$DR$ increases as either microgroove spacing  $w$ or
$w$ or  $Re$ increases. The velocity fields obtained using particle image velocimetry indicate that the air-filled SHP grooves induce a considerable wall slip. This slip significantly weakens the intensity of Taylor rolls, reduces local momentum transport, and consequently lowers drag. This phenomenon becomes more pronounced with increasing
$Re$ increases. The velocity fields obtained using particle image velocimetry indicate that the air-filled SHP grooves induce a considerable wall slip. This slip significantly weakens the intensity of Taylor rolls, reduces local momentum transport, and consequently lowers drag. This phenomenon becomes more pronounced with increasing  $w$. Furthermore, to quantify the multiscale relationship between global response and geometrical as well as driving parameters,
$w$. Furthermore, to quantify the multiscale relationship between global response and geometrical as well as driving parameters,  $DR\sim (w, \phi _s, Re)$, a theoretical model is established based on angular momentum defect theory and magnitude estimate. It is demonstrated that a decrease in the surface solid fraction can reduce wall shear, and an increase in the groove width can weaken turbulence kinetic energy production, rendering enhanced slip and drag reduction. This research has implications for designing and optimizing turbulent-drag-reducing surfaces in various engineering applications, such as transportation and marine engineering.
$DR\sim (w, \phi _s, Re)$, a theoretical model is established based on angular momentum defect theory and magnitude estimate. It is demonstrated that a decrease in the surface solid fraction can reduce wall shear, and an increase in the groove width can weaken turbulence kinetic energy production, rendering enhanced slip and drag reduction. This research has implications for designing and optimizing turbulent-drag-reducing surfaces in various engineering applications, such as transportation and marine engineering.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 2
- Cited by


