Article contents
Freely rising or falling of a sphere in a square tube at intermediate Reynolds numbers
Published online by Cambridge University Press: 02 December 2024
Abstract
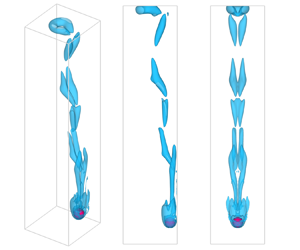
The motion of a sphere freely rising or falling in a 5d (d is the diameter of the sphere) square tube was numerically studied for the sphere-to-fluid density ratio ranging from 0.1 to 2.3 (0.1 ≤ ρs/ρ ≤ 2.3, ρs is the density of spheres and ρ the fluid density) and Galileo number from 140 to 230 (140 ≤ Ga ≤ 230). We report that Hopf bifurcation occurs at Gacrit ≈ 157, where both the heavy and light spheres lose stability. The helical motion is widely seen for all spheres at Ga > 160 resulting from a double-threaded vortex interacting with the tube walls, which becomes irregular at Ga ≥ 190 where heavy spheres act differently from their counterparts; that is, heavy spheres change their helical directions alternately while light spheres exhibit helical trajectories with jaggedness in connection with the shedding of the double-threaded vortices. This is because of the difference in inertia between the heavy and light spheres. We also checked the oscillation periods for the helical motion of the spheres. They show opposite variations with ρs/ρ for the two types of spheres. Light spheres (ρs/ρ ≤ 0.7) reach a zigzagging regime at Ga ≥ 200 where a vortex loop (hairpin-like vortical structure) is formed which may develop into a vortex ring downstream at small ρs/ρ. This might be the first time a transition from the helical motion to the zigzagging motion for heavy spheres (ρs/ρ ≥ 1.8) has been reported. Finally, we examined the dependence of both the terminal Reynolds number and the drag coefficient of the spheres on the Galileo number.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by


