3.1. Increasing the rotation rate to suppress the Föppl vortices

Figure 2. Snapshots of the wake with overlaid streamlines and vorticity plots for varying rotation rates at ${Re} = 20$ and $\alpha / F = 20$ . The vorticity range is $-25$ to 25 s $^{-1}$ . These snapshots are captured when the cylinder is at the end of its CW rotation and is about to start rotating in the CCW direction, i.e. an instantaneous rotation rate of zero.

We first focus on the influence of the forced periodic rotation on the cylinder’s near wake and observe how these forced rotations influence the formation of the Föppl vortices. Snapshots of the near wake for increasing rotation rate are shown in figure 2 for rotation rates varying from $\alpha =0$ to $\alpha =4$ , while keeping the Reynolds number and the maximum angular displacement constant at ${Re}=20$ and $\alpha /F=20$ , respectively. These snapshots correspond to the moment when the cylinder has stopped rotating in the clockwise (CW) direction and is about to start rotating in the CCW direction, i.e. at an instantaneous angular velocity of zero. For $\alpha =0$ , symmetric Föppl vortices are observed in the near wake as expected (figure 2 a). Slightest rotation breaks the flow symmetry in the wake and the Föppl vortices are suppressed over a major portion of the rotation period. The Föppl vortices appear only momentarily when the instantaneous angular velocity is zero. For $\alpha =0.3$ , the bottom Föppl vortex does not exist at this instant of time, even in the form of a very small vortex, and the top vortex is reduced in size since the flow is deflected more by the larger rotation rates (figure 2 b). The size of the momentarily observed upper Föppl vortex reduces with increasing rotation rate to $\alpha =0.5$ . For $\alpha =1$ (figure 2 d), the upper Föppl vortex becomes diminishingly small. The Föppl vortices disappear completely for rotation rates larger than $\alpha =1$ , as shown for sample cases of $\alpha =2$ and $\alpha =4$ in figure 2(e,f).

3.2. Decreasing $\alpha /F$ to suppress the Föppl vortices

Figure 3. Streamline plots around a cylinder periodically rotating at a rotation rate of $\alpha =0.5$ , a constant Reynolds number of ${Re}=40$ and for three different values of $\alpha /F$ . These snapshots are captured at the end of the CW rotation.

For larger Reynolds numbers within the subcritical range, the size of the Föppl vortices increases. Earlier, we demonstrated that these larger Föppl vortices can be suppressed completely by increasing the rotation rate while keeping $\alpha /F$ constant. Here, we show that for a constant rotation rate, $\alpha$ , we can suppress the Föppl vortices by decreasing $\alpha / F$ (i.e. increasing the forcing frequency). Figure 3 shows the near wake of the cylinder at ${Re}=40$ as a sample case, as the cylinder is forced to rotate at three distinct dimensionless rotation frequencies of $\alpha /F=20$ , 10 and 6.7. A Föppl vortex is observed in the re-circulation region for $\alpha /F=20$ (figure 3 a). When $\alpha /F$ is decreased to $\alpha /F=10$ by increasing the forcing frequency, $f$ , the bottom Föppl vortex becomes smaller, but still a large vortex is formed on the upper side of the cylinder, which travels downstream before it dissipates (figure 3 b). Both of these vortices disappear from the near wake when $\alpha /F$ is further decreased to $\alpha /F=6.7$ (figure 3 c).

3.3. Mechanisms of vortex formation and dissipation in the near wake

Figure 4. Overlaid snapshots of streamlines and vorticity for (a–d) ${Re}=20$ and $\alpha /F = 20$ ; (e–h) ${Re}=40$ and $\alpha /F = 20$ ; and (i–l) ${Re}=20$ and $\alpha /F = 10$ , at different instances over one cycle of rotation. The rotation rate for all these cases is $\alpha = 0.5$ . The vorticity range is $-25$ to $25$ s $^{-1}$ . In each column, the cycle of periodic rotation is shown in the first row by plotting the normalised angular velocity during the cycle. The markers on the plot indicate the instances when the snapshots are taken.

In general, we have observed three mechanisms for the formation and dissipation of vortices in the near wake when the cylinder is forced to rotate periodically. Figure 4 shows snapshots that correspond to samples for these three mechanisms.

The snapshots in figure 4(a–d) correspond to a case with ${Re}=20$ , $\alpha /F = 20$ and $\alpha =0.5$ . Figure 4(a) corresponds to an instance when the cylinder reaches its maximum rotation rate in the CCW direction. Moving from panels (a) to (b), the rotation rate is reduced, while the cylinder keeps rotating in the CCW direction. As the cylinder slows down, the influence of cylinder rotation remains localised in space, and the streamlines far from the cylinder straighten out and follow the incoming flow. The streamlines close to the cylinder curve due to the influence of rotation, and as a result, a vortex originates filling the gap between the curved streamlines and the straight streamlines (figure 4 b). The formation of this vortex differs from the typical Föppl vortex formation in the case of a fixed cylinder as this vortex does not form exactly behind the cylinder. As the cylinder’s rotation slows down further (moving from the panels bto c), this vortex grows in size and moves upstream, as the reduced rotation rate of the cylinder does not influence the streamlines enough to curve and therefore more streamlines straighten out causing the re-circulation region to become wider. As the cylinder reaches zero angular velocity (panel d), the vortex reaches the cylinder and its size reduces, since the CCW rotation of the cylinder that was feeding the vortex earlier has now become zero and the dominant direction of curving of the streamlines has changed. This vortex disappears completely as the cylinder starts rotating in the CW direction.

For the same rotation rate and frequency, but at a higher Reynolds number of ${Re}\,{=}\,40$ , shown in figure 4(e–h), the streamlines that pass the lower side of the cylinder go further downstream before turning and following the cylinder’s CCW rotation (figure 4 e). This creates S-shaped streamlines near the cylinder and, as the rotation slows down, the re-circulation zone becomes longer and the S-shape becomes flatter. In addition to the previously observed CW vortex at the top, we now observe a weak CCW vortex underneath the CW vortex (figure 4 f). Following a similar phenomenon discussed in the previous case for ${Re}=20$ , the top vortex grows and moves upstream, causing the bottom vortex to move downstream as the cylinder rotation further slows down (figure 4 g). As the cylinder rotation reaches zero angular velocity, the top vortex reaches the cylinder and reduces in size (figure 4 h), and the bottom vortex moves downstream and is shed.

In figure 4(i–l), we consider the case of ${Re}=20$ and $\alpha =0.5$ , at a dimensionless rotation frequency of $\alpha /F = 10$ . In this case, we do not observe an upstream-moving vortex when the cylinder rotation slows down, since the smaller $\alpha /F$ (larger frequency) does not provide enough time for the vortex to form and move upstream. Instead, we observe a vortex in the re-circulation region very close to the cylinder as the cylinder switches the direction of rotation from CW to CCW (figure 4 i). As the cylinder starts its CCW rotation, the streamlines move along with the cylinder, detaching the vortex and forcing it to move downstream (figure 4 j). The vortex then disappears as the angular velocity is increased (figure 4 k,l).

4.1. Inducing vortices by varying $\alpha /F$

Figure 5. Vorticity contours for varying $\alpha /F$ at three different rotation rates, (a) $\alpha =1$ , (b) $\alpha =1.5$ and (c) $\alpha =2$ . For all these cases, ${Re}=20$ . In each column, $\alpha /F$ decreases from top to bottom. The vorticity ranges from $-5$ to 5 s $^{-1}$ . These snapshots are captured at the end of the CW rotation.

First, we consider the cases where we keep the Reynolds number constant at ${Re}=20$ and impose a rotation at a constant rotation rate, $\alpha =1$ , 1.5 or 2, and decreasing $\alpha /F$ , i.e. increasing rotation frequency (top to bottom in figure 5). To decrease $\alpha /F$ , the dimensional frequency $f$ is increased while maintaining a constant angular velocity, $\omega$ . Then, as the frequency is increased, the maximum angle of rotation is decreased. For the largest $\alpha /F$ , as shown in figure 5 (first row), $\alpha /F=200$ , the shear layers extend downstream and they are minimally disrupted by the forced rotation as the dimensional frequency is very small. Weak vortex shedding is observed at $\alpha =2$ . With decreasing $\alpha /F$ (increasing dimensional frequency), these long shear layers start interacting with each other due to imposed periodic rotation and vortices are shed in the wake. Decreasing $\alpha /F$ at a constant angular velocity, $\omega$ , results in a reduction in the maximum angular displacement. Consequently, the size of the vortices that are shed in the wake decreases (moving from top to bottom in figure 5). The vortex-shedding frequency follows the rotation frequency, $f$ . For smaller values of $\alpha /F$ (e.g. $\alpha /F=13$ and $\alpha /F=20$ for $\alpha =1$ and $\alpha =1.5$ , respectively), the shed vortices become much smaller. For the lowest values of $\alpha /F$ shown in the figure (i.e. the highest forcing frequencies tested here), the periodic rotation merely perturbs the shear layers and the vortex shedding ceases, since the maximum angle of rotation becomes extremely small. Therefore, it becomes clear that whether or not shedding is observed in the wake depends on the combination of the rotation rate and rotation frequency. This range is highlighted in the figure.

4.2. Inducing vortices by varying the rotation rate

Vortices can also be induced by varying the rotation rate at a constant $\alpha /F$ . In figure 6, vorticity plots are shown for increasing rotation rates at $\alpha /F=40$ . Inducing vortices in the wake at subcritical Reynolds number does not occur for very small rotation rates, which is evident from figure 6(a). By increasing the rotation rate from $\alpha =0.5$ to $\alpha =1$ , vortex shedding is observed in the wake. The vortex shedding becomes prominent with further increase in the rotation rate (e.g. $\alpha =1.5$ and $\alpha =2$ ). It is important to note that the rotation rate is increased while keeping the Reynolds number and $\alpha /F$ constant. The dimensional frequency must also increase to maintain constant $\alpha /F$ with increasing rotation rate, $\alpha$ . Therefore, the vortex-shedding frequency increases with increasing rotation rate. At large values of rotation rate, $\alpha =3$ and $\alpha =4$ , the shed vortices are much smaller in size and they coalesce in the far wake as seen in figures 6(e) and 6(f). Increasing the rotation rate further will cause the vortex shedding to cease and only the perturbations in the shear layers will be observed. The window where vortex shedding is observed moves to larger values of rotation rate, $\alpha$ , with increasing $\alpha /F$ , as depicted in figure 5. It becomes clear from these results that one should control both $\alpha$ and $\alpha /F$ to induce vortex shedding with a desired strength, a desired size and a desired shedding frequency within the subcritical Reynolds number range.

Figure 6. Vorticity plots for varying rotation rates, $\alpha$ , at $\alpha /F=40$ . The Reynolds number is fixed at ${Re}=20$ for all cases. The colourbar range is –5 to 5 ${\rm s}^{-1}$ .

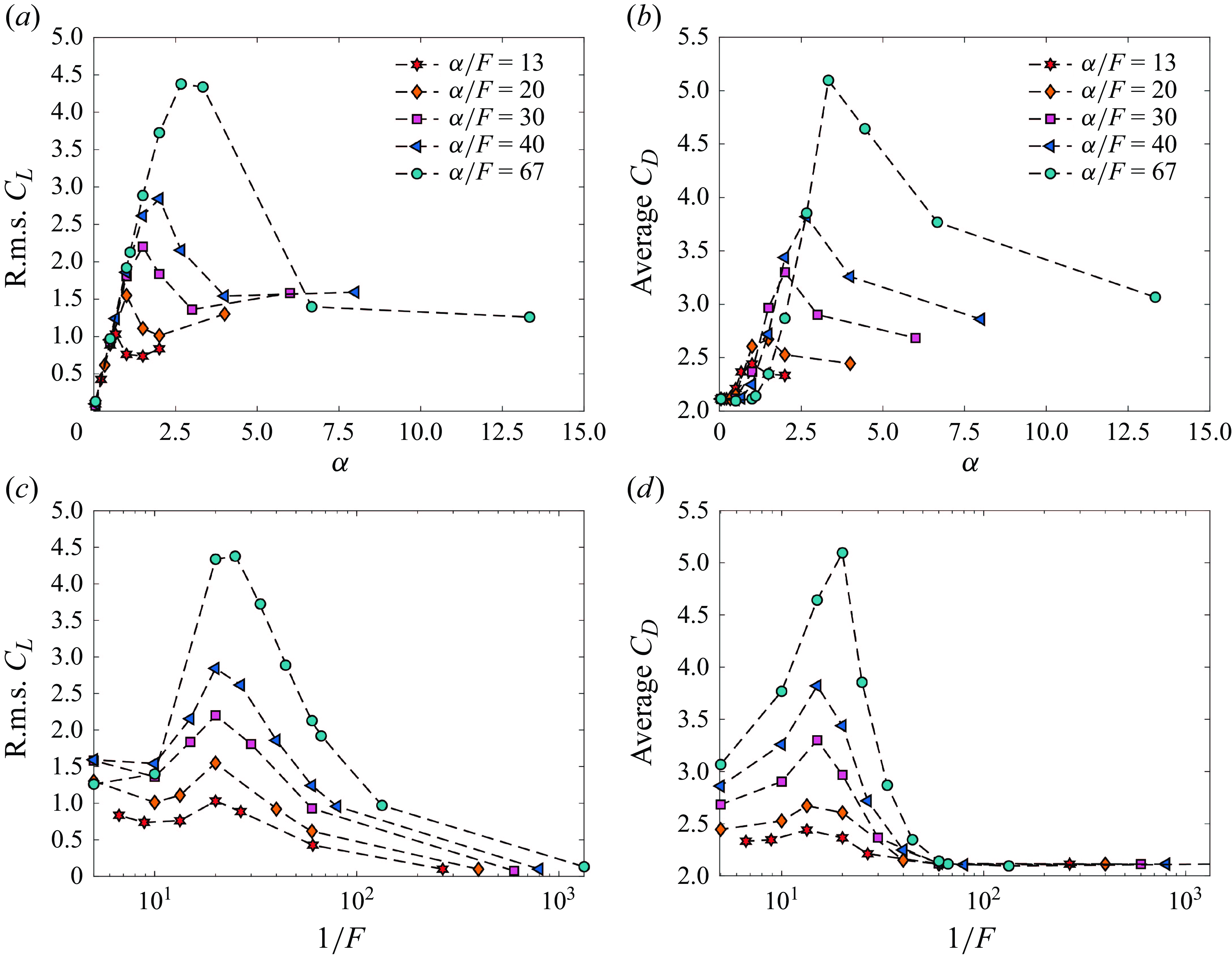
Figure 7. Root-mean-square lift coefficient versus (a) rotation rate, $\alpha$ , and (c) $1/F$ for varying $\alpha /F$ . The average drag coefficient versus (b) rotation rate, $\alpha$ , and (d) $1/F$ for varying $\alpha /F$ . The Reynolds number is ${Re}=20$ for all cases.

4.3. Lift and drag forces imposed on the cylinder

Figure 8. Time-averaged pressure distribution on a cylinder shown as a coefficient of pressure ( $C_p$ ) versus the angle ( $\theta$ ) for $\alpha /F=40$ . The angle $\theta =0$ is defined at the upstream side of the cylinder, where the incoming flow first encounters the cylinder surface. The angle $\theta$ increases in the clockwise direction around the cylinder. The Reynolds number is ${Re}=20$ for all cases.

As vortices are formed in the wake of the cylinder forced to rotate periodically, fluctuating lift forces act on the cylinder. In figure 7(a), the r.m.s. (root mean square) of the lift coefficient is plotted against the rotation rate, $\alpha$ , for different forcing frequencies, represented as $\alpha /F$ . For the highest rotation frequency, $\alpha /F=13$ , the r.m.s. lift increases when the rotation rate is increased to $\alpha =0.5$ , as vortices start to form. It peaks at $\alpha =0.67$ and then decreases slightly with a further increase in the rotation rate. For $\alpha \gt 0.5$ , the r.m.s. lift increases with increasing $\alpha /F$ due to the larger vortices that are shed at higher values of $\alpha /F$ (as seen in figure 5). With increasing $\alpha /F$ , the r.m.s. lift peaks at a larger value of $\alpha$ . These maxima occur at $\alpha =1$ , $1.5$ , $2$ and $2.67$ for $\alpha /F=20$ , $30$ , $40$ and $67$ , respectively. This trend is observed because the vortex shedding occurs at a larger value of rotation rate, $\alpha$ , with increasing $\alpha /F$ , as shown previously in figure 5. For all values of  $\alpha /F$ , the drop in the r.m.s. lift that is observed for larger values of rotation rate corresponds to the weaker vortex shedding caused by the increased dimensional frequency at larger values of rotation rate.

The average drag coefficient is plotted against $\alpha$ for varying $\alpha /F$ in figure 7(b). A trend similar to that observed in the plot of the r.m.s. $C_L$ is observed here. At a constant $\alpha$ , the average drag coefficient increases with increasing $\alpha /F$ . For a constant $\alpha /F$ , the average $C_D$ increases with increasing $\alpha$ , reaches a peak and decreases with further increase in the rotation rate. This behaviour can be understood by plotting the pressure distribution on the cylinder for varying rotation rates at a constant $\alpha /F$ . In figure 8, the coefficient of pressure, $C_p$ , is plotted against the angle, $\theta$ , for a sample case of $\alpha /F=40$ . The coefficient of pressure is time-averaged, since the cylinder is rotating periodically. The area over the $C_p$ curve in figure 8 quantifies the pressure drag component of the overall drag coefficient, $C_D$ . For $\alpha =0.66$ , two separation points are observed (recognised by the change in sign of the slope of the $C_p$ curve) and the area over the $C_p$ curve is the smallest. This case corresponds to the smallest average $C_D$ among all four rotation rates shown in figure 8. With increasing the rotation rate to $\alpha =2$ , the angle between the two separation points decreases. At $\alpha =2.66$ , flow separation does not occur as both separation points merge and the area over the $C_p$ curve is the largest. Therefore, the average $C_D$ peaks at $\alpha =2.66$ . With increasing the rotation rate to $\alpha =4$ , two separation points reappear because the cylinder rotates at a larger angular velocity in a clockwise or counterclockwise direction for a shorter period of time to maintain constant $\alpha /F$ . Therefore, the area over the $C_p$ curve for $\alpha =4$ is smaller compared with for $\alpha =2.66$ , signifying the drop in the average $C_D$ after peaking at $\alpha =2.66$ .

In the plots in figure 7(a,b), we observe that the maximum fluctuating lift and mean drag occur at progressively larger values of $\alpha$ , for increasing $\alpha /F$ . If, instead of plotting these values versus $\alpha$ , we plot them versus $\alpha /F$ divided by $\alpha$ , i.e. $1/F$ (figures 7 c and 7 d), then the peak r.m.s. $C_L$ occurs at a constant $1/F = 20$ for all $\alpha /F$ cases and the peak of the mean drag coefficients occurs at a value between $1/F=15$ and $1/F=20$ .

This new variable $1/F$ can also be written as

(4.1) \begin{equation} \frac {1}{F} = \frac {2U}{fD} = U^* .\end{equation}

The variable $2U/(fD)$ is very similar to the reduced velocity, $U^*$ , commonly found in the literature of flow-induced vibrations (Williamson & Govardhan Reference Williamson and Govardhan2004; Patel Reference Patel2024). As the incoming velocity, $U$ , and the cylinder diameter, $D$ , remain constant for the cases shown in figure 7, the variable $U^*$ is inversely proportional to the frequency of the rotational oscillations, $f$ .

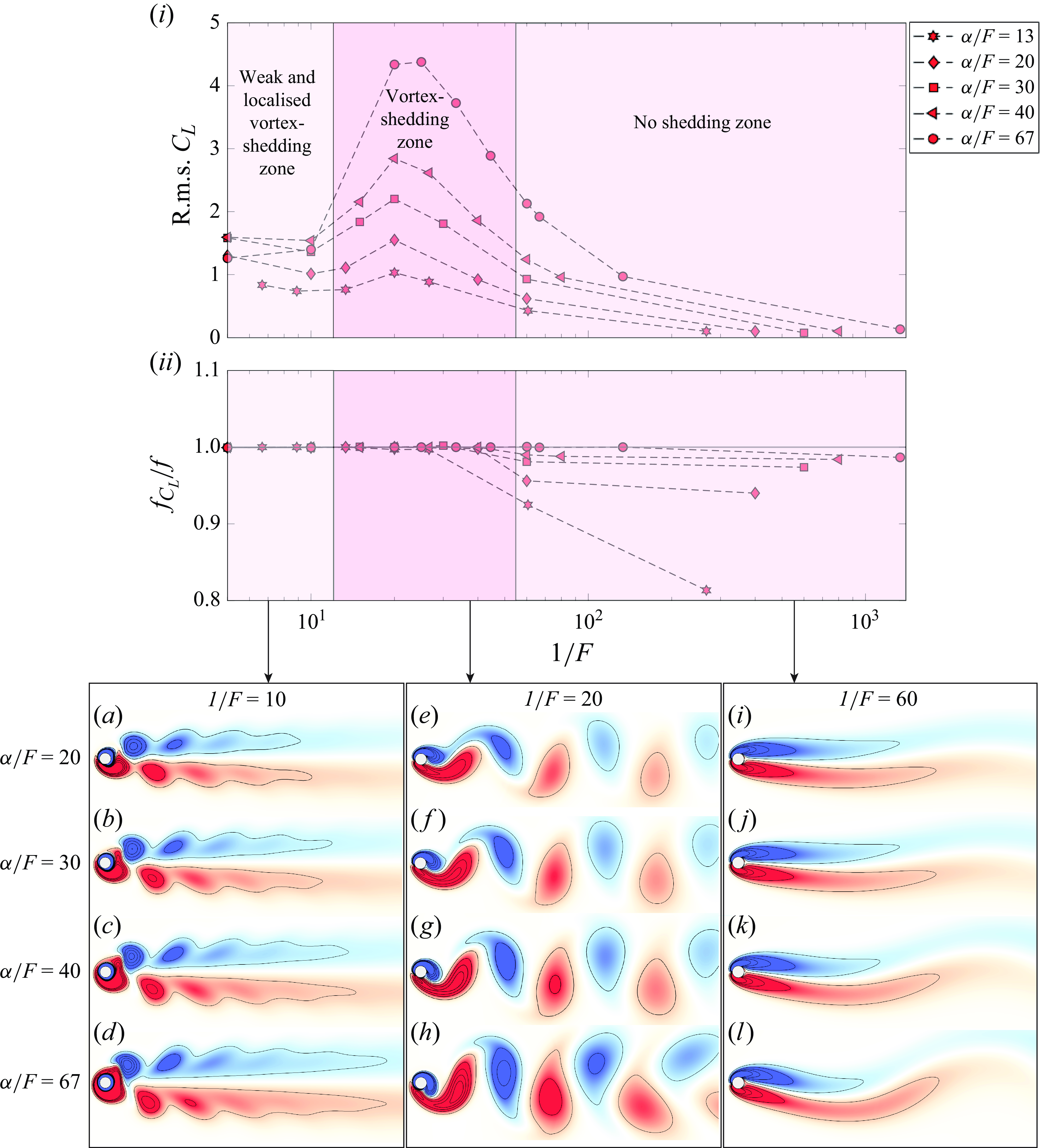
Figure 9. (i) Fluctuating lift force and (ii) peak frequency of the lift force time history normalised by the forcing frequency versus $1/F$ . Three zones with three different wake patterns are observed in the wake of a cylinder forced to rotate periodically (highlighted in the plots). Samples of the vorticity contours are shown in the lower panels: for (a–d) $1/F=10$ ; (e–h) $1/F = 20$ ;, and (i–l) $1/F = 60$ for varying $\alpha /F$ . The Reynolds number is fixed at ${Re}=20$ for all cases. The colourbar range is from −5 to 5 ${\rm s}^{-1}$ .

In figure 9(a–l), vorticity contours are plotted over a range of $1/F$ values and for various $\alpha /F$ values. The Reynolds number is kept constant for all cases at ${Re}=20$ . Based on the observed vorticity patterns, we can categorise the observed wakes into three distinct zones. For lower values of $1/F$ , the vortices are weak and observed only in the close proximity of the cylinder. Due to the high frequency of cylinder rotation within this range, vortices are separated quickly from the cylinder before being fully formed, merely perturbing the shear layers. Such vorticity patterns are observed for any combination of $\alpha$ and $\alpha /F$ values leading to small values of $1/F$ (approximately less than 12). This region is highlighted in figure 9(i) as the weak and localised vortex-shedding zone. At larger values of $1/F$ , where the frequency of rotation is reduced, we observe a pattern similar to the von Kármán vortex street over a range of $1/F$ values. This region is highlighted as the vortex-shedding zone in figure 9(i). Vortex shedding is observed for any combination of $\alpha$ and $\alpha /F$ values leading to moderate values of $1/F$ (approximately in the range of $12\lt 1/F\lt 55$ ). At higher values of $1/F$ (approximately greater than 55), i.e. lower rotation frequencies, vortex shedding ceases completely. In this range, the shear layers stretch far downstream and vortices are not formed in the near wake. This region is highlighted as the no shedding zone in figure 9(i). Clearly, the range of high-amplitude fluctuating lift forces corresponds to the vortex-shedding zone where fully formed vortices are shed in the near wake of the cylinder due to the forced rotation and exert relatively large fluctuating lift forces on the structure. The forced rotation causes the fluctuations in the shear layers and, in some cases, the formation of vortices. The frequency of the fluctuations in the lift force caused by the periodic rotation is calculated through the FFT (fast Fourier transform) of the lift force time history. This frequency is indicated by $f_{C_L}$ . The sustained global instability is caused by the lock-in between the frequency of periodic rotation and $f_{C_L}$ . If the frequency of periodic rotation is too high, then only localised instability is observed and the vortices dissipate quickly. If the frequency of periodic rotation is too low, then vortices are not formed. Therefore, this lock-in is the cause for the global wake instability. This is confirmed in figure 9(ii), where we plot $f_{C_L}/f$ versus $1/F$ . This ratio stays equal to 1 when sustained shedding is observed.

4.4. Minimum Reynolds number to induce vortices in the wake

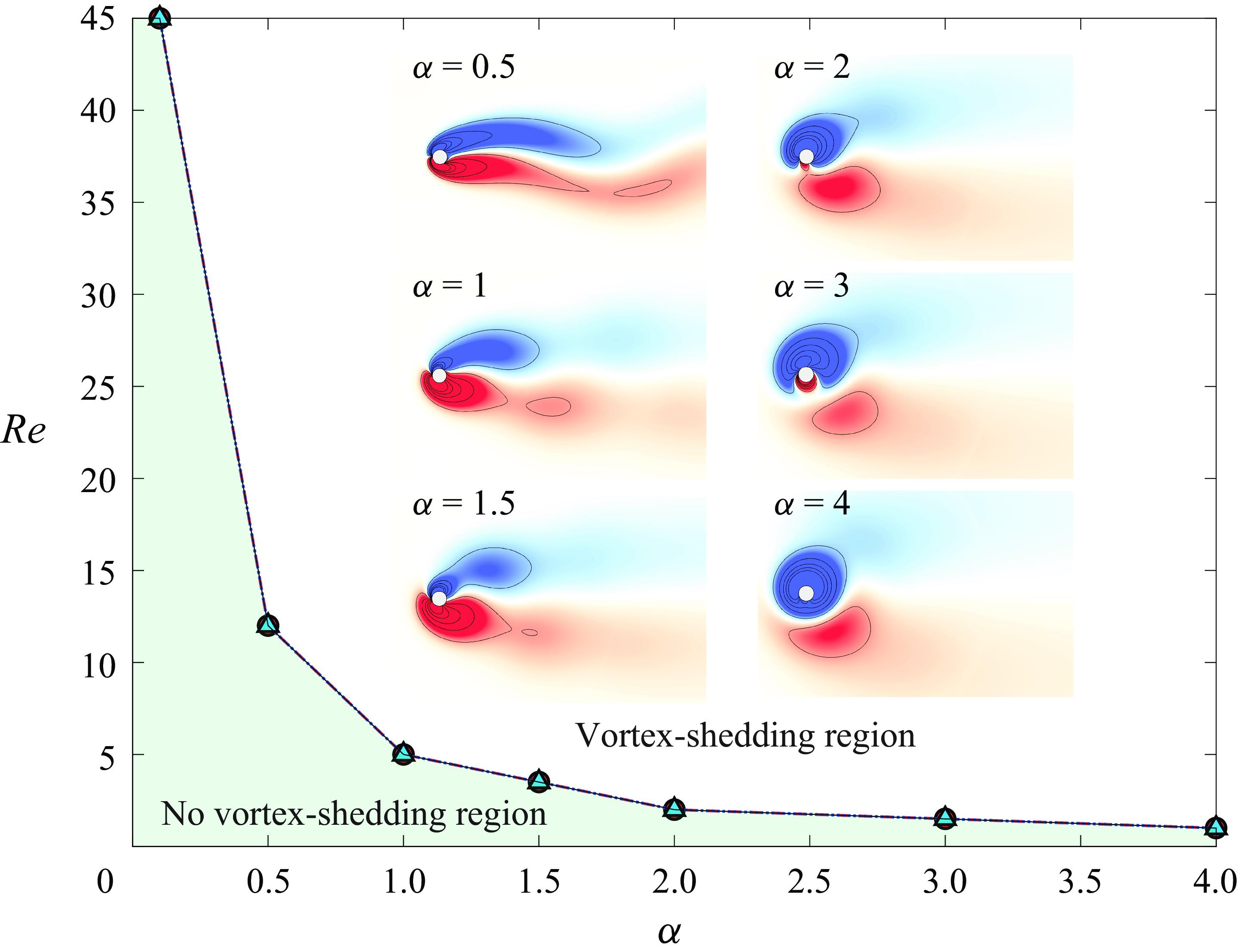
Figure 10. Critical Reynolds number to observe vortex shedding in the wake of a cylinder forced to rotate periodically versus the rotation rate, $\alpha$ . The ratio $\alpha /F \equiv \omega /f$ is kept constant while two sets of values for $\omega$ and $f$ are considered in such a way that their ratio remains the same, i.e. $\omega _1/f_1 = \omega _2/f_2 = 20$ , where $\omega _1\neq \omega _2$ and $f_1\neq f_2$ . Red and blue markers in the plot correspond to these two combinations of $\alpha /F$ . The snapshots indicate the vorticity contours at the critical Reynolds numbers for the onset of shedding for each case. The vorticity range is –3 to 3 ${\rm s}^{-1}$ . See the Supplementary movies of the wake for cases of $\alpha =2$ , ${Re}=2$ and $\alpha =4$ , ${Re}=1$ .

In previous sections, we observed that the vortices can be induced in the wake of a cylinder at subcritical Reynolds numbers when the cylinder is forced to rotate periodically. The question then arises as to what is the minimum Reynolds number at which these vortices can be induced. In figure 10, we show that this minimum Reynolds number for the onset of induced vortices in the wake of the cylinder depends on the rotation rate. As the rotation rate is increased, vortices can be induced in the wake at lower Reynolds numbers. At lower $\alpha$ values, the critical Reynolds number to impose shedding in the wake increases to values larger than 45. As $\alpha$ is increased, this critical value decreases quickly to values smaller than 10. We have observed vortex shedding at ${Re}=1$ for $\alpha =4$ . Due to the imposed rotation, the local Reynolds number near the cylinder is larger than the Reynolds number based on the incoming flow velocity. The maximum Reynolds number can be described by ${Re}_{max} = {Re} (1+\alpha )$ . By increasing the rotation rate, the amount of vorticity that is generated is increased and a bound vortex is formed. At lower Reynolds numbers, this bound vortex would have stayed attached if the direction of rotation had not been switched since the ${Re}_{max}$ does not exceed the critical Reynolds number for vortex shedding ( ${Re}_{cr} = 47$ ). When we change the direction of rotation, the bound vortex is forced to separate and shed in the wake. In the insets of figure 10, we show the vorticity plots for a range of rotation rates at their respective critical Reynolds numbers for the onset of vortex shedding. The plot shown in figure 10 corresponds to $\alpha /F=20$ . We have considered two different combinations of $\omega$ and $f$ to get $\alpha /F=20$ : $\omega =40 \;{\rm rad\,s}^{-1}$ and $f=2 \; {\rm Hz}$ (red markers) and $\omega =80 \; {\rm rad\,s}^{-1}$ and $f=4 \; {\rm Hz}$ (blue markers). Both of these combinations yield the same critical Reynolds number to observe vortex shedding in the wake at a constant rotation rate as the red and blue lines are identical, as shown in figure 10. Therefore, it is the ratio of angular velocity, $\omega$ , and rotation frequency, $f$ , ( $\omega /f \equiv \alpha /F$ ) that is important to be considered to pinpoint the minimum Reynolds number for the onset of shedding, and not $\omega$ or $f$ .