Article contents
Flame wrinkle destruction processes in harmonically forced, turbulent premixed flames
Published online by Cambridge University Press: 19 March 2013
Abstract
This paper describes analyses of the nonlinear dynamics of harmonically forced, turbulent premixed flames. A key objective of this work is to analyse the ensemble-averaged dynamics of the flame front position, 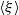 $\langle \xi \rangle $ , excited by harmonic forcing of amplitude
$\langle \xi \rangle $ , excited by harmonic forcing of amplitude  $\varepsilon $ , in the presence of stochastic flow fluctuations of amplitude
$\varepsilon $ , in the presence of stochastic flow fluctuations of amplitude 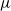 $\mu $ . Low-amplitude and/or near-field effects are quantified by a third-order perturbation analysis, while the more general case is analysed computationally by solving the three-dimensional level-set equation, extracting the instantaneous flame position, and ensemble averaging the results. We show that different mechanisms contribute to smoothing of flame wrinkles, manifested as progressive decay in the magnitude of
$\mu $ . Low-amplitude and/or near-field effects are quantified by a third-order perturbation analysis, while the more general case is analysed computationally by solving the three-dimensional level-set equation, extracting the instantaneous flame position, and ensemble averaging the results. We show that different mechanisms contribute to smoothing of flame wrinkles, manifested as progressive decay in the magnitude of  $\langle \xi \rangle $ . Near the flame holder, random phase jitter, associated with stochastic velocity fluctuations tangential to the flame, is dominant. Farther downstream, propagation of the ensemble-averaged front normal to itself at the time-averaged turbulent burning velocity,
$\langle \xi \rangle $ . Near the flame holder, random phase jitter, associated with stochastic velocity fluctuations tangential to the flame, is dominant. Farther downstream, propagation of the ensemble-averaged front normal to itself at the time-averaged turbulent burning velocity, 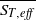 $ \overline{{S}_{T, eff} } $ , leads to destruction of wrinkles, analogous to the laminar case, an effect that scales with
$ \overline{{S}_{T, eff} } $ , leads to destruction of wrinkles, analogous to the laminar case, an effect that scales with 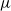 $\mu $ . A second, new result is the demonstration that the ensemble-averaged turbulent burning velocity,
$\mu $ . A second, new result is the demonstration that the ensemble-averaged turbulent burning velocity,  ${S}_{T, eff} (s, t)$ , is modulated by the harmonic forcing, i.e.
${S}_{T, eff} (s, t)$ , is modulated by the harmonic forcing, i.e. 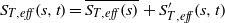 ${S}_{T, eff} (s, t)= \overline{{S}_{T, eff} (s)} + { S}_{T, eff}^{\prime } (s, t)$ , where
${S}_{T, eff} (s, t)= \overline{{S}_{T, eff} (s)} + { S}_{T, eff}^{\prime } (s, t)$ , where 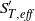 ${ S}_{T, eff}^{\prime } $ has an inverse dependence upon the instantaneous, ensemble averaged-flame curvature, an effect that scales with
${ S}_{T, eff}^{\prime } $ has an inverse dependence upon the instantaneous, ensemble averaged-flame curvature, an effect that scales with  $\varepsilon $ and
$\varepsilon $ and 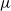 $\mu $ . We show that this curvature dependence follows from basic application of Huygens propagation to flames with stochastic wrinkling superimposed upon base curvature. This effect also leads to smoothing of flame wrinkles and is analogous to stretch processes in positive-Markstein-length, laminar flames.
$\mu $ . We show that this curvature dependence follows from basic application of Huygens propagation to flames with stochastic wrinkling superimposed upon base curvature. This effect also leads to smoothing of flame wrinkles and is analogous to stretch processes in positive-Markstein-length, laminar flames.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 38
- Cited by

