Article contents
Finite-amplitude instabilities of thin internal wave beams: experiments and theory
Published online by Cambridge University Press: 07 October 2020
Abstract
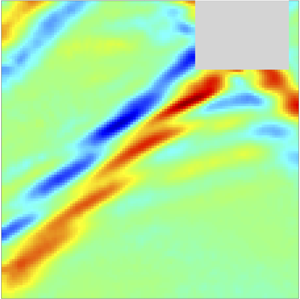
A joint experimental and theoretical study is made of instability mechanisms of locally confined internal gravity wave beams in a stratified fluid. Using as forcing a horizontal cylinder that is oscillated harmonically in the direction of beam propagation makes it possible to generate coherent finite-amplitude internal wave beams whose spatial profile comprises no more than a single wavelength. For forcing amplitude above a certain threshold depending on the driving frequency, such thin wave beams are observed to undergo an instability that involves two subharmonic perturbations with wavepacket-like spatial structure. Although it bears resemblance to the triadic resonant instability (TRI) of small-amplitude sinusoidal waves, the present instability cannot be predicted by TRI theory as the primary wave is not nearly monochromatic, but instead contains broadband wavenumber spectrum. In contrast, the experimental observations are in good agreement with the predictions of a formal linear stability analysis based on Floquet theory. Finally, experimental evidence is presented that transverse beam variations induce a horizontal mean flow of the streaming type and greatly subdue the instability.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 14
- Cited by


