Article contents
Faxén formulas for particles of arbitrary shape and material composition
Published online by Cambridge University Press: 11 January 2021
Abstract
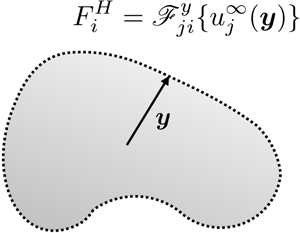
We prove a duality between the functional forms of the Faxén formulas associated with a particle of a given shape and material composition and the corresponding singularity solutions for the velocity disturbances induced by that particle, and extend it to the case of systems with coupled transport processes, enabling the solution of a large family of problems via Faxén methods. Prior approaches to constructing proofs of duality of Faxén formulas and Stokes-flow singularities relied on knowledge of all boundary conditions on all particle surfaces, viz. the Lorentz reciprocal theorem approach. We recognized that, in order to bypass the complexity of boundary conditions one can instead invoke energy methods that give reciprocity between operators rather than between specific stress and velocity fields. We derive reciprocal relations between operators, from which we demonstrate that the Faxén/singularity duality is a consequence of a generalized reciprocal relation between conjugate thermodynamic variables. We use our reciprocal relations to derive expressions for the hydrodynamic force on a sphere of arbitrary composition, the hydrodynamic stresslet exerted on a deformable droplet in an arbitrary velocity field, the phoretic force exerted on a rigid particle in the thin double-layer limit in response to arbitrary externally imposed field and the total stresslet on a charged particle in an arbitrary velocity field, i.e. an electroviscous Faxén law.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by

