Published online by Cambridge University Press: 17 January 2017
This paper presents both linear and nonlinear analyses of extreme responses for a multi-body wave energy converter (WEC) in severe sea states. The WEC known as M4 consists of three cylindrical floats with diameters and draft which increase from bow to stern with the larger mid and stern floats having rounded bases so that the overall system has negligible drag effects. The bow and mid float are rigidly connected by a beam and the stern float is connected by a beam to a hinge above the mid float where the rotational relative motion would be damped to absorb power in operational conditions. A range of focussed wave groups representing extreme waves were tested on a scale model without hinge damping, also representing a more general system of interconnected cylindrical floats with multi-mode forcing. Importantly, the analysis reveals a predominantly linear response structure in hinge angle and weakly nonlinear response for the beam bending moment, while effects due to drift forces, expected to be predominantly second order, are not accounted for. There are also complex and violent free-surface effects on the model during the excitation period driven by the main wave group, which generally reduce the overall motion response. Once the main group has moved away, the decaying response in the free-vibration phase decays at a rate very close to that predicted by simple linear radiation damping. Two types of nonlinear harmonic motion are demonstrated. During the free-vibration phase, there are only double and triple frequency Stokes harmonics of the linear motion, captured using a frequency doubling and tripling model. In contrast, during the excitation phase, these harmonics show much more complex behaviour associated with nonlinear fluid loading. Although bound harmonics are visible in the system response, the overall response is remarkably linear until temporary submergence of the central float (‘dunking’) occurs. This provides a strong stabilising effect for angular amplitudes greater than 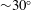 ${\sim}30^{\circ }$ and can be treated as a temporary loss of part of the driving wave as long as submergence continues. With an experimentally and numerically derived response amplitude operator (RAO), we perform a statistical analysis of extreme response for the hinge angle based on wave data at Orkney, well known for its severe wave climate, using the NORA10 wave hindcast. For storms with spectral peak wave periods longer than the RAO peak period, the response is controlled by the steepness of the sea state rather than the wave height. Thus, the system responds very similarly under the most extreme sea states, providing an upper bound for the most probable maximum response, which is reduced significantly in directionally spread waves. The methodology presented here is relevant to other single and multi-body systems including WECs. We also demonstrate a general and potentially important reciprocity result for linear body motion in random seas: the averaged wave history given an extreme system response and the average response history given an extreme wave match in time, with time reversed for one of the signals. This relationship will provide an efficient and robust way of defining a ‘designer wave’, for both experimental testing and computationally intensive computational fluid dynamics (CFD), for a wide range of wave–structure interaction problems.
${\sim}30^{\circ }$ and can be treated as a temporary loss of part of the driving wave as long as submergence continues. With an experimentally and numerically derived response amplitude operator (RAO), we perform a statistical analysis of extreme response for the hinge angle based on wave data at Orkney, well known for its severe wave climate, using the NORA10 wave hindcast. For storms with spectral peak wave periods longer than the RAO peak period, the response is controlled by the steepness of the sea state rather than the wave height. Thus, the system responds very similarly under the most extreme sea states, providing an upper bound for the most probable maximum response, which is reduced significantly in directionally spread waves. The methodology presented here is relevant to other single and multi-body systems including WECs. We also demonstrate a general and potentially important reciprocity result for linear body motion in random seas: the averaged wave history given an extreme system response and the average response history given an extreme wave match in time, with time reversed for one of the signals. This relationship will provide an efficient and robust way of defining a ‘designer wave’, for both experimental testing and computationally intensive computational fluid dynamics (CFD), for a wide range of wave–structure interaction problems.