Article contents
External turbulence-induced axial flow and instability in a vortex
Published online by Cambridge University Press: 16 March 2016
Abstract
External turbulence-induced axial flow in an incompressible, normal-mode stable Lamb–Oseen (two-dimensional) vortex column is studied via direct numerical simulations of the Navier–Stokes equations. Azimuthally oriented vorticity filaments, formed from external turbulence, advect radially towards or away from the vortex axis (depending on the filament’s swirl direction), resulting in a net induced axial flow in the vortex core; axial flow increases with increasing vortex Reynolds number ( 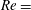 $Re=$ vortex circulation/viscosity). This contrasts the viscous mechanism for axial flow generation downstream of a lifting body, wherein an axial pressure gradient is produced by viscous diffusion of the swirl (Batchelor, J. Fluid Mech., vol. 20, 1964, pp. 645–658). Analysis of the self-induced motion of an arbitrarily curved external filament shows that any non-axisymmetric filament undergoes radial advection. We then studied the evolution of a vortex column starting with an imposed optimal transient growth perturbation. For a range of Re values, axial flow develops and initially grows as (time)
$Re=$ vortex circulation/viscosity). This contrasts the viscous mechanism for axial flow generation downstream of a lifting body, wherein an axial pressure gradient is produced by viscous diffusion of the swirl (Batchelor, J. Fluid Mech., vol. 20, 1964, pp. 645–658). Analysis of the self-induced motion of an arbitrarily curved external filament shows that any non-axisymmetric filament undergoes radial advection. We then studied the evolution of a vortex column starting with an imposed optimal transient growth perturbation. For a range of Re values, axial flow develops and initially grows as (time) 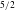 $^{5/2}$ before decreasing after two turnover times; for
$^{5/2}$ before decreasing after two turnover times; for  $Re=10\,000$ – the highest computationally achievable – axial flow at late times becomes sufficiently strong to induce vortex instability. Contrary to a prior claim of a parent–offspring mechanism at the outer edge of the core, vorticity tilting within the core by axial flow is the underlying mechanism producing energy growth. Thus, external perturbations in practical flows (at
$Re=10\,000$ – the highest computationally achievable – axial flow at late times becomes sufficiently strong to induce vortex instability. Contrary to a prior claim of a parent–offspring mechanism at the outer edge of the core, vorticity tilting within the core by axial flow is the underlying mechanism producing energy growth. Thus, external perturbations in practical flows (at 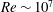 $Re\sim 10^{7}$ ) produce destabilizing axial flow, possibly leading to the sought-after vortex breakup.
$Re\sim 10^{7}$ ) produce destabilizing axial flow, possibly leading to the sought-after vortex breakup.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 7
- Cited by


