Hostname: page-component-7857688df4-92hv7 Total loading time: 0 Render date: 2025-11-15T07:41:03.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental study of the convection in a rotating tangent cylinder

Published online by Cambridge University Press:  21 March 2018

Kélig Aujogue Open the ORCID record for Kélig Aujogue [Opens in a new window] ,
Alban Pothérat ,
Binod Sreenivasan Open the ORCID record for Binod Sreenivasan [Opens in a new window]  and
François Debray
Kélig Aujogue*
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV15FB, UK
Alban Pothérat
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV15FB, UK
Binod Sreenivasan
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560 012, India
François Debray
Affiliation:
Laboratoire National des Champs Magnétiques Intenses-Grenoble, CNRS/UGA-UPS-INSA, France
*
†Email address for correspondence: aujogue.kelig@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper experimentally investigates the convection in a rapidly rotating tangent cylinder (TC), for Ekman numbers down to 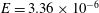$E=3.36\times 10^{-6}$. The apparatus consists of a hemispherical fluid vessel heated in its centre by a protruding heating element of cylindrical shape. The resulting convection that develops above the heater, i.e. within the TC, is shown to set in for critical Rayleigh numbers and wavenumbers respectively scaling as 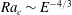$Ra_{c}\sim E^{-4/3}$ and 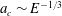$a_{c}\sim E^{-1/3}$ with the Ekman number 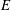$E$. Although exhibiting the same exponents as for plane rotating convection, these laws reflect much larger convective plumes at onset. The structure and dynamics of supercritical plumes are in fact closer to those found in solid rotating cylinders heated from below, suggesting that the confinement within the TC induced by the Taylor–Proudman constraint influences convection in a similar way as solid walls would do. There is a further similarity in that the critical modes in the TC all exhibit a slow retrograde precession at onset. In supercritical regimes, the precession evolves into a thermal wind with a complex structure featuring retrograde rotation at high latitude and either prograde or retrograde rotation at low latitude (close to the heater), depending on the criticality and the Ekman number. The intensity of the thermal wind measured by the Rossby number 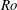$Ro$ scales as 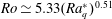$Ro\simeq 5.33(Ra_{q}^{\ast })^{0.51}$ with the Rayleigh number based on the heat flux 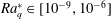$Ra_{q}^{\ast }\in [10^{-9},10^{-6}]$. This scaling is in agreement with heuristic predictions and previous experiments where the thermal wind is determined by the azimuthal curl of the balance between the Coriolis force and buoyancy. Within the range 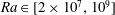$Ra\in [2\times 10^{7},10^{9}]$ which we explored, we also observe a transition in the heat transfer through the TC from a diffusivity-free regime where 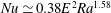$Nu\simeq 0.38E^{2}Ra^{1.58}$ to a rotation-independent regime where 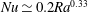$Nu\simeq 0.2Ra^{0.33}$.

JFM classification

Convection: Convection Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Rotating flows

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 355 - 381
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aubert, J. 2005 Steady zonal flows in spherical shell dynamos. J. Fluid Mech. 542, 53–67.Google Scholar
Aubert, J., Brito, D., Nataf, H.-C., Cardin, P. & Masson, J.-P. 2001 A systematic experimental study of rapidly rotating spherical convection in water and liquid gallium. Phys. Earth Planet. Inter. 128 (1), 51–74.Google Scholar
Aujogue, K., Pothérat, A., Bates, I., Debray, F. & Sreenivasan, B. 2016 Little earth experiment: an instrument to model planetary cores. Rev. Sci. Instrum. 87 (8), 084502.Google Scholar
Aujogue, K., Pothérat, A. & Sreenivasan, B. 2015 Onset of plane layer magnetoconvection at low Ekman number. Phys. Fluids 27 (10), 106602.Google Scholar
Aurnou, J. 2007 Planetary core dynamics and convective heat transfer scaling. Geophys. Astrophys. Fluid Dyn. 101 (5–6), 327–345.Google Scholar
Aurnou, J., Andreadis, S., Zhu, L. & Olson, P. 2003 Experiments on convection in Earth’s core tangent cylinder. Earth Planet. Sci. Lett. 212 (1), 119–134.Google Scholar
Aurnou, J. M. & Olson, P. 2001 Experiments on Rayleigh–Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.Google Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44 (03), 441–460.Google Scholar
Cardin, P. & Olson, P. 1994 Chaotic thermal convection in a rapidly rotating spherical shell: consequences for flow in the outer core. Phys. Earth Planet. Inter. 82 (3–4), 235–259.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press.Google Scholar
Cheng, J. S. & Aurnou, J. M. 2016 Tests of diffusion-free scaling behaviors in numerical dynamo datasets. Earth Planet. Sci. Lett. 436, 121–129.Google Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201 (1), 1–17.Google Scholar
Christensen, U. R. 2002 Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 470, 115–133.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166 (1), 97–114.Google Scholar
Clune, T. & Knoblauch, E. 1993 Pattern selection in rotating convection with experimental boundary conditions. Phys. Rev. E 47 (4), 2536–2540.Google Scholar
Cui, A. & Street, R. L. 2001 Large-eddy simulation of turbulent rotating convective flow development. J. Fluid Mech. 447, 53–84.Google Scholar
Curbelo, J., Lopez, J. M., Mancho, A. M. & Marques, F. 2014 Confined rotating convection with large Prandtl number: centrifugal effects on wall modes. Phys. Rev. E 89, 013019.Google Scholar
Ecke, R. E., Zhong, F. & Knobloch, E. 1992 Hopf bifurcation with broken reflection symmetry in rotating Rayleigh–Bénard convection. Europhys. Lett. 19 (3), 177–182.Google Scholar
Gastine, T., Wicht, J. & Aubert, J. 2016 Scaling regimes in spherical shell rotating convection. J. Fluid Mech. 808, 690–732.Google Scholar
Gastine, T., Wicht, J. & Aurnou, J. M. 2015 Turbulent Rayleigh–Bénard convection in spherical shells. J. Fluid Mech. 778, 721–764.Google Scholar
Glatzmaiers, G. A. & Roberts, P. H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203–209.Google Scholar
Goldstein, H. F., Knoblauch, E., Mercader, I. & Net, M. 1994 Convection in a rotating cylinder. Part 2. Linear theory for low Prandtl numbers. J. Fluid Mech. 262, 293–324.Google Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Hollerbach, R. 1994 Imposing a magnetic field across a nonaxisymmetric shear layer in a rotating spherical shell. Phys. Fluids 6 (7), 2540–2544.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26, 055111.Google Scholar
Hulot, G., Eymin, C., Langlais, B., Mandea, M. & Olsen, N. 2002 Small-scale structure of the geodynamo inferred from oersted and magsat satellite data. Nature 416 (6881), 620–623.Google Scholar
Jacobs, P. & Ivey, G. N. 1998 The influence of rotation on shelf convection. J. Fluid Mech. 369, 23–48.Google Scholar
Jones, C. A. 2007 Thermal and compositional convection in the outer core. In Treatise in Geophysics, Core Dynamics, vol. 8, pp. 131–185. Elsevier.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012 Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (25), 254503.Google Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.Google Scholar
de Koker, N., Steinle-Neumann, G. & Vlček, V. 2012 Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earths core. Proc. Natl Acad. Sci. USA 109 (11), 4070–4073.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Kunnen, R. P. J., Geurts, B. J. & Clerx, H. J. H. 2010 Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 642, 445–476.Google Scholar
Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., van Heijst, G. F. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.Google Scholar
Livermore, P. W. & Hollerbach, R. 2012 Successive elimination of shear layers by a hierarchy of constraints in inviscid spherical-shell flows. J. Math. Phys. 53 (7), 073104.Google Scholar
Livermore, P. W., Hollerbach, R. & Finlay, C. 2017 An accelerating high-latitude jet in earths core. Nat. Geo. 10, 62–69.Google Scholar
Marques, F., Mercader, I., Batiste, O. & Lopez, J. M. 2007 Centrifugal effects in rotating convection: axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 580, 303–318.Google Scholar
Maxworthy, T. & Narimousa, S. 1994 Unsteady turbulent convection into a homogeneous rotating fluid with oceanic applications. J. Phys. Oceanogr. 24, 865–887.Google Scholar
Pozzo, M., Davies, C., Gubbins, D. & Alfe, D. 2012 Thermal and electrical conductivity of iron at earth’s core conditions. Nature 485 (7398), 355–358.Google Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 10.1093/gji/ggx265.Google Scholar
Schubert, G. & Soderlund, K. M. 2011 Planetary magnetic fields: observations and models. Phys. Earth Planet. Inter. 187 (3), 92–108.Google Scholar
Sreenivasan, B. & Jones, C. A. 2006 Azimuthal winds, convection and dynamo action in the polar regions of planetary cores. Geophys. Astrophys. Fluid Dyn. 100 (4–5), 319–339.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3 (1), 17–26.Google Scholar
Sumita, I. & Olson, P. 2003 Experiments on highly supercritical thermal convection in a rapidly rotating hemispherical shell. J. Fluid Mech. 492, 271–287.Google Scholar
Trümper, T., Breuer, M. & Hansen, U. 2012 Numerical study on double-diffusive convection in the earths core. Phys. Earth Planet. Inter. 194, 55–63.Google Scholar
Zhang, K. & Liao, X. 2009 The onset of convection in rotating circular cylinders with experimental boundary conditions. J. Fluid Mech. 622, 63–73.Google Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.Google Scholar
Supplementary material: File

Aujogue et al. supplementary material

Aujogue et al. supplementary material 1

Download Aujogue et al. supplementary material(File)
File 14.8 KB