Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lee, Y.J.
Zhou, G.
and
Lua, K.B.
2019.
Two-dimensional numerical study of isotoxal-star polygonal cylinders in cross-flow.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 188,
Issue. ,
p.
125.
Li, Sen
Li, Ruoning
Wang, Zunce
Xu, Dekui
Yan, Yuejuan
Xu, Yan
Li, Jingshuai
and
Chen, Xing
2019.
Fluid-Structure Interaction Vibration Response Analysis of the Hydrocyclone Under Periodic Excitation.
IEEE Access,
Vol. 7,
Issue. ,
p.
146273.
Wang, Qing-Yang
Xu, Sheng-Jin
Gan, Lian
Zhang, Wei-Guo
and
Zhou, Yu
2019.
Scaling of the time-mean characteristics in the polygonal cylinder near-wake.
Experiments in Fluids,
Vol. 60,
Issue. 12,
Wang, Qingyang
Gan, Lian
Xu, Shengjin
and
Zhou, Yu
2020.
Vortex evolution in the near wake behind polygonal cylinders.
Experimental Thermal and Fluid Science,
Vol. 110,
Issue. ,
p.
109940.
Masoudi, Esmaeel
Gan, Lian
and
Sims-Williams, David
2021.
Large eddy simulation of incident flows around polygonal cylinders.
Physics of Fluids,
Vol. 33,
Issue. 10,
Yang, Yong-liang
Guo, Rui
Liu, Rong-zhong
Chen, Liang
Xing, Bo-yang
and
Zhao, Bo-bo
2021.
Quasi-steady aerodynamic characteristics of Terminal Sensitive Bullets with short cylindrical portion.
Defence Technology,
Vol. 17,
Issue. 2,
p.
633.
Lekkala, Malakonda Reddy
Latheef, Mohamed
Jung, Jae Hwan
Coraddu, Andrea
Zhu, Hongjun
Srinil, Narakorn
Lee, Byung-Hyuk
and
Kim, Do Kyun
2022.
Recent advances in understanding the flow over bluff bodies with different geometries at moderate Reynolds numbers.
Ocean Engineering,
Vol. 261,
Issue. ,
p.
111611.
Mishra, Shravan Kumar
Yadav, Pavan Kumar
Sarkar, Himalaya
and
Sen, Subhankar
2022.
Correspondence between the number of no-slip critical points and nature of rear stagnation point of a symmetric object.
Physics of Fluids,
Vol. 34,
Issue. 11,
Solanki, Dhaval T
and
Sharma, Dharmendra S
2022.
Potential flow around polygonal shaped cylinders using hypotrochoidal mapping function.
International Journal of Mechanical Sciences,
Vol. 226,
Issue. ,
p.
107395.
Vakhshouri, Mir Elyad
and
Çuhadaroğlu, Burhan
2022.
Effects of uniform injection and suction through perforated pentagonal cylinders on the flow and heat transfer.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 32,
Issue. 4,
p.
1324.
Forouzi Feshalami, Behzad
He, Shuisheng
Scarano, Fulvio
Gan, Lian
and
Morton, Chris
2022.
A review of experiments on stationary bluff body wakes.
Physics of Fluids,
Vol. 34,
Issue. 1,
Solanki, Dhaval T.
and
Sharma, Dharmendra S.
2023.
Hydrodynamic interaction between two polygonal cylinders in uniform potential flow.
Ocean Engineering,
Vol. 286,
Issue. ,
p.
115674.
2023.
Evidence and physical mechanism for vortex-induced vibration of a bluff body without an afterbody.
Physics of Fluids,
Vol. 35,
Issue. 6,
Masoudi, Esmaeel
Sims-Williams, David
and
Gan, Lian
2023.
Flow separation from polygonal cylinders in an incident flow.
Physical Review Fluids,
Vol. 8,
Issue. 1,
Orlando, Andrea
Pagnini, Luisa
and
Pia Repetto, Maria
2023.
Wind tunnel tests of a hexadecagonal cylinder with imperfections and ancillaries: aerodynamic characterization and technical discussion.
Engineering Structures,
Vol. 274,
Issue. ,
p.
115114.
Nouri, Saliha
Boulaaras, Salah
and
Hafsia, Zouhaier
2023.
Vortex shedding induced by polygonal cylinders.
The European Physical Journal Special Topics,
Vol. 232,
Issue. 4,
p.
403.
Cheng, Hao
Masoudi, Esmaeel
Liu, Yu
and
Gan, Lian
2024.
On the asymmetric vortex evolution in the near wake behind polygonal cylinders in an incident flow.
Ocean Engineering,
Vol. 307,
Issue. ,
p.
118142.
Angle, Brandon R.
Rau, Matthew J.
and
Byron, Margaret L.
2024.
Settling of nonuniform cylinders at intermediate Reynolds numbers.
Physical Review Fluids,
Vol. 9,
Issue. 7,
Wang, Ran
Cheng, Shaohong
and
Ting, David S.K.
2024.
Comparison of Pressure-based and Skin Friction-based Methods for the
Determination of Flow Separation of a Circular Cylinder with Roundness
Imperfection.
Current Chinese Science,
Vol. 4,
Issue. 3,
p.
159.
Zhou, Yu
Hao, Jingcheng
and
Alam, Md. Mahbub
2024.
Wake of two tandem square cylinders.
Journal of Fluid Mechanics,
Vol. 983,
Issue. ,
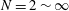 $N=2\sim \infty$ is systematically studied based on fluid force, hot-wire, particle image velocimetry and flow visualisation measurements. Each cylinder is examined for two orientations, with a flat surface or a corner leading and facing normally to the free stream. The Reynolds number
$N=2\sim \infty$ is systematically studied based on fluid force, hot-wire, particle image velocimetry and flow visualisation measurements. Each cylinder is examined for two orientations, with a flat surface or a corner leading and facing normally to the free stream. The Reynolds number 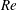 $Re$ is
$Re$ is 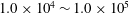 $1.0\times 10^{4}\sim 1.0\times 10^{5}$, based on the longitudinally projected cylinder width. The time-averaged drag coefficient
$1.0\times 10^{4}\sim 1.0\times 10^{5}$, based on the longitudinally projected cylinder width. The time-averaged drag coefficient 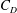 $C_{D}$ and fluctuating lift coefficient on these cylinders are documented, along with the characteristic properties including the Strouhal number
$C_{D}$ and fluctuating lift coefficient on these cylinders are documented, along with the characteristic properties including the Strouhal number 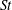 $St$, flow separation point and angle
$St$, flow separation point and angle 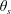 $\unicode[STIX]{x1D703}_{s}$, wake width and critical Reynolds number
$\unicode[STIX]{x1D703}_{s}$, wake width and critical Reynolds number 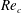 $Re_{c}$ at which the transition from laminar to turbulent flow occurs. It is found that once
$Re_{c}$ at which the transition from laminar to turbulent flow occurs. It is found that once 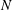 $N$ exceeds 12,
$N$ exceeds 12, 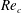 $Re_{c}$ depends on the difference between the inner diameter (tangent to the faces) and the outer diameter (connecting corners) of a polygon, the relationship being approximately given by the dependence of
$Re_{c}$ depends on the difference between the inner diameter (tangent to the faces) and the outer diameter (connecting corners) of a polygon, the relationship being approximately given by the dependence of 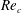 $Re_{c}$ on the height of the roughness elements for a circular cylinder. It is further found that
$Re_{c}$ on the height of the roughness elements for a circular cylinder. It is further found that 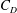 $C_{D}$ versus
$C_{D}$ versus 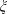 $\unicode[STIX]{x1D709}$ or
$\unicode[STIX]{x1D709}$ or 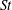 $St$ versus
$St$ versus 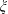 $\unicode[STIX]{x1D709}$ for all the tested cases collapse onto a single curve, where the angle
$\unicode[STIX]{x1D709}$ for all the tested cases collapse onto a single curve, where the angle 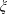 $\unicode[STIX]{x1D709}$ is the corrected
$\unicode[STIX]{x1D709}$ is the corrected 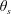 $\unicode[STIX]{x1D703}_{s}$ associated with the laterally widest point of the polygon and the separation point. Finally, the empirical correlation between
$\unicode[STIX]{x1D703}_{s}$ associated with the laterally widest point of the polygon and the separation point. Finally, the empirical correlation between  $C_{D}$ and
$C_{D}$ and 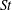 $St$ is discussed.
$St$ is discussed.