Article contents
Experimental investigation of intermittent airflow separation and microscale wave breaking in wavy two-phase pipe flow
Published online by Cambridge University Press: 18 September 2019
Abstract
We perform an experimental analysis of co-current, stratified wavy pipe flow, with the aim of investigating the effect of small scale wave breaking (microscale breaking) on the airflow. Particle image velocimetry is applied simultaneously in the gas and liquid phases. Active wave breaking is identified by high levels of vorticity on the leeward side of individual waves, and the statistics of the airflow above breaking and non-breaking waves are extracted from the gas-phase velocity fields. Keeping the liquid superficial velocity constant ( $U_{sl}=0.1~\text{m}~\text{s}^{-1}$), we consider two experimental cases of different gas flow rates. The lowest flow rate (
$U_{sl}=0.1~\text{m}~\text{s}^{-1}$), we consider two experimental cases of different gas flow rates. The lowest flow rate (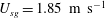 $U_{sg}=1.85~\text{m}~\text{s}^{-1}$) is slightly higher than the onset of microscale breaking, while the higher flow rate (
$U_{sg}=1.85~\text{m}~\text{s}^{-1}$) is slightly higher than the onset of microscale breaking, while the higher flow rate ( $U_{sg}=2.20~\text{m}~\text{s}^{-1}$) is within the regime where wave breaking is observed to be frequent, and the root-mean-square interface elevation
$U_{sg}=2.20~\text{m}~\text{s}^{-1}$) is within the regime where wave breaking is observed to be frequent, and the root-mean-square interface elevation  $\unicode[STIX]{x1D702}_{rms}$ is independent of gas flow rate. Results show that for the lowest gas flow rate considered, active wave breaking has a stabilizing effect on the airflow above the waves, reducing the sheltered region on the leeward side of the wave and the turbulence above the wave crest compared with non-breaking waves at similar steepness. At the higher gas flow rate the effect of active wave breaking is found to be small, and the main geometrical properties of the waves are found to dominate the evolution of the separated flow region.
$\unicode[STIX]{x1D702}_{rms}$ is independent of gas flow rate. Results show that for the lowest gas flow rate considered, active wave breaking has a stabilizing effect on the airflow above the waves, reducing the sheltered region on the leeward side of the wave and the turbulence above the wave crest compared with non-breaking waves at similar steepness. At the higher gas flow rate the effect of active wave breaking is found to be small, and the main geometrical properties of the waves are found to dominate the evolution of the separated flow region.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 8
- Cited by

