Article contents
Experimental investigation of flow-induced vibration of a sinusoidally rotating circular cylinder
Published online by Cambridge University Press: 05 June 2018
Abstract
The present experimental investigation characterises the dynamic response and wake structure of a sinusoidally rotating circular cylinder with a low mass ratio (defined as the ratio of the total oscillating mass to the displaced fluid mass) undergoing cross-stream flow-induced vibration (FIV). The study covers a wide parameter space spanning the forcing rotary oscillation frequency ratio 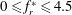 $0\leqslant f_{r}^{\ast }\leqslant 4.5$ and the forcing rotation speed ratio
$0\leqslant f_{r}^{\ast }\leqslant 4.5$ and the forcing rotation speed ratio 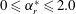 $0\leqslant \unicode[STIX]{x1D6FC}_{r}^{\ast }\leqslant 2.0$ , at reduced velocities associated with the vortex-induced vibration (VIV) upper and lower amplitude response branches. Here,
$0\leqslant \unicode[STIX]{x1D6FC}_{r}^{\ast }\leqslant 2.0$ , at reduced velocities associated with the vortex-induced vibration (VIV) upper and lower amplitude response branches. Here, 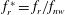 $f_{r}^{\ast }=f_{r}/f_{nw}$ and
$f_{r}^{\ast }=f_{r}/f_{nw}$ and 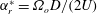 $\unicode[STIX]{x1D6FC}_{r}^{\ast }=\unicode[STIX]{x1D6FA}_{o}D/(2U)$ , where
$\unicode[STIX]{x1D6FC}_{r}^{\ast }=\unicode[STIX]{x1D6FA}_{o}D/(2U)$ , where 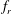 $f_{r}$ is the forcing rotary oscillation frequency,
$f_{r}$ is the forcing rotary oscillation frequency, 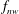 $f_{nw}$ is the natural frequency of the system in quiescent fluid (water),
$f_{nw}$ is the natural frequency of the system in quiescent fluid (water), 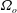 $\unicode[STIX]{x1D6FA}_{o}$ is the peak angular rotation speed,
$\unicode[STIX]{x1D6FA}_{o}$ is the peak angular rotation speed, 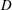 $D$ is the cylinder diameter and
$D$ is the cylinder diameter and 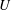 $U$ is the free-stream velocity; the reduced velocity is defined by
$U$ is the free-stream velocity; the reduced velocity is defined by 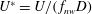 $U^{\ast }=U/(\,f_{nw}D)$ . The fluid–structure system was modelled using a low-friction air-bearing system in conjunction with a free-surface recirculating water channel, with axial rotary motion provided by a microstepping motor. The cylinder was allowed to vibrate with only one degree of freedom transverse to the oncoming free-stream flow. It was found that in specific ranges of
$U^{\ast }=U/(\,f_{nw}D)$ . The fluid–structure system was modelled using a low-friction air-bearing system in conjunction with a free-surface recirculating water channel, with axial rotary motion provided by a microstepping motor. The cylinder was allowed to vibrate with only one degree of freedom transverse to the oncoming free-stream flow. It was found that in specific ranges of 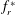 $f_{r}^{\ast }$ , the body vibration frequency may deviate from that seen in the non-rotating case and lock onto the forcing rotary oscillation frequency or its one-third subharmonic. The former is referred to as the ‘rotary lock-on’ (RLO) region and the latter as the ‘tertiary lock-on’ (TLO) region. Significant increases in the vibration amplitude and suppression of VIV could both be observed in different parts of the RLO and TLO regions. The peak amplitude response in the case of
$f_{r}^{\ast }$ , the body vibration frequency may deviate from that seen in the non-rotating case and lock onto the forcing rotary oscillation frequency or its one-third subharmonic. The former is referred to as the ‘rotary lock-on’ (RLO) region and the latter as the ‘tertiary lock-on’ (TLO) region. Significant increases in the vibration amplitude and suppression of VIV could both be observed in different parts of the RLO and TLO regions. The peak amplitude response in the case of 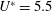 $U^{\ast }=5.5$ (upper branch) was observed to be
$U^{\ast }=5.5$ (upper branch) was observed to be 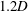 $1.2D$ , an increase of approximately
$1.2D$ , an increase of approximately 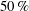 $50\,\%$ over the non-rotating case, while in the case of
$50\,\%$ over the non-rotating case, while in the case of 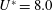 $U^{\ast }=8.0$ (lower branch), the peak amplitude response was
$U^{\ast }=8.0$ (lower branch), the peak amplitude response was 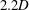 $2.2D$ , a remarkable increase of
$2.2D$ , a remarkable increase of 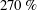 $270\,\%$ over the non-rotating case. Notably, the results showed that the amplitude responses at moderate Reynolds numbers (
$270\,\%$ over the non-rotating case. Notably, the results showed that the amplitude responses at moderate Reynolds numbers (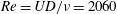 $Re=UD/\unicode[STIX]{x1D708}=2060$ and
$Re=UD/\unicode[STIX]{x1D708}=2060$ and 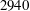 $2940$ , where
$2940$ , where  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) in the present study showed significant differences from those of a previous low-Reynolds-number (
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) in the present study showed significant differences from those of a previous low-Reynolds-number (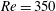 $Re=350$ ) numerical study at similar reduced velocities by Du & Sun (Phys. Fluids, vol. 14 (8), 2015, pp. 2767–2777). Remarkably, in an additional study examining the cylinder vibration as a function of
$Re=350$ ) numerical study at similar reduced velocities by Du & Sun (Phys. Fluids, vol. 14 (8), 2015, pp. 2767–2777). Remarkably, in an additional study examining the cylinder vibration as a function of 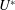 $U^{\ast }$ while the fixed forcing rotary oscillation parameters were kept constant at
$U^{\ast }$ while the fixed forcing rotary oscillation parameters were kept constant at 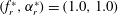 $(f_{r}^{\ast },\unicode[STIX]{x1D6FC}_{r}^{\ast })=(1.0,1.0)$ , the cylinder experienced substantially larger oscillations than in the non-rotating case, and a rotation-induced galloping response was observed for
$(f_{r}^{\ast },\unicode[STIX]{x1D6FC}_{r}^{\ast })=(1.0,1.0)$ , the cylinder experienced substantially larger oscillations than in the non-rotating case, and a rotation-induced galloping response was observed for 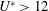 $U^{\ast }>12$ , where the amplitude increased monotonically to reach approximately
$U^{\ast }>12$ , where the amplitude increased monotonically to reach approximately 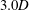 $3.0D$ at the highest reduced velocity (
$3.0D$ at the highest reduced velocity (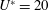 $U^{\ast }=20$ ) tested. Furthermore, new wake modes were identified in the RLO and TLO regions using particle image velocimetry measurements at selected points in the
$U^{\ast }=20$ ) tested. Furthermore, new wake modes were identified in the RLO and TLO regions using particle image velocimetry measurements at selected points in the 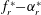 $f_{r}^{\ast }-\unicode[STIX]{x1D6FC}_{r}^{\ast }$ parameter space.
$f_{r}^{\ast }-\unicode[STIX]{x1D6FC}_{r}^{\ast }$ parameter space.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Wong et al. supplementary movie 1
Phase-averaged vorticity contours showing the 2Po pattern at (fr∗, αr∗) = (1.0, 1.0) in the RLO region of the U∗ = 5.5 case.
Wong et al. supplementary movie 2
Phase-averaged vorticity contours showing the 2S pattern at (fr∗, αr∗) = (1.0, 2.0) in the U∗ = 5.5 case.
Wong et al. supplementary movie 3
Phase-averaged vorticity contours showing the 2S pattern at (fr∗, αr∗) = (3.0, 2.0) in the U∗ = 5.5 case.
Wong et al. supplementary movie 4
Phase-averaged vorticity contours showing the 4S pattern at (fr∗, αr∗) = (3.0, 1.0) in the TLO region of the U∗ = 5.5 case.
- 35
- Cited by


