Article contents
Experimental characterization of three-dimensional corner flows at low Reynolds numbers
Published online by Cambridge University Press: 19 July 2012
Abstract
We investigate experimentally the characteristics of the flow field that develops at low Reynolds numbers (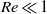 ) around a sharp
) around a sharp 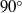 corner bounded by channel walls. Two-dimensional planar velocity fields are obtained using particle image velocimetry (PIV) conducted in a towing tank filled with a silicone oil of high viscosity. We find that, in the vicinity of the corner, the steady-state flow patterns bear the signature of a three-dimensional secondary flow, characterized by counter-rotating pairs of streamwise vortical structures and identified by the presence of non-vanishing transverse velocities (
corner bounded by channel walls. Two-dimensional planar velocity fields are obtained using particle image velocimetry (PIV) conducted in a towing tank filled with a silicone oil of high viscosity. We find that, in the vicinity of the corner, the steady-state flow patterns bear the signature of a three-dimensional secondary flow, characterized by counter-rotating pairs of streamwise vortical structures and identified by the presence of non-vanishing transverse velocities (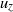 ). These results are compared to numerical solutions of the incompressible flow as well as to predictions obtained, for a similar geometry, from an asymptotic expansion solution (Guglielmini et al., J. Fluid Mech., vol. 668, 2011, pp. 33–57). Furthermore, we discuss the influence of both Reynolds number and aspect ratio of the channel cross-section on the resulting secondary flows. This work represents, to the best of our knowledge, the first experimental characterization of the three-dimensional flow features arising in a pressure-driven flow near a corner at low Reynolds number.
). These results are compared to numerical solutions of the incompressible flow as well as to predictions obtained, for a similar geometry, from an asymptotic expansion solution (Guglielmini et al., J. Fluid Mech., vol. 668, 2011, pp. 33–57). Furthermore, we discuss the influence of both Reynolds number and aspect ratio of the channel cross-section on the resulting secondary flows. This work represents, to the best of our knowledge, the first experimental characterization of the three-dimensional flow features arising in a pressure-driven flow near a corner at low Reynolds number.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 5
- Cited by

