Article contents
Evolution of thermally stratified turbulent open channel flow after removal of the heat source
Published online by Cambridge University Press: 01 August 2019
Abstract
Evolution of thermally stratified open channel flow after removal of a volumetric heat source is investigated using direct numerical simulation. The heat source models radiative heating from above and varies with height due to progressive absorption. After removal of the heat source the initial stable stratification breaks down and the channel approaches a fully mixed isothermal state. The initial state consists of three distinct regions: a near-wall region where stratification plays only a minor role, a central region where stratification has a significant effect on flow dynamics and a near-surface region where buoyancy effects dominate. We find that a state of local energetic equilibrium observed in the central region of the channel in the initial state persists until the late stages of the destratification process. In this region local turbulence parameters such as eddy diffusivity 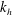 $k_{h}$ and flux Richardson number
$k_{h}$ and flux Richardson number 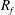 $R_{f}$ are found to be functions only of the Prandtl number
$R_{f}$ are found to be functions only of the Prandtl number 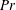 $Pr$ and a mixed parameter
$Pr$ and a mixed parameter 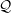 ${\mathcal{Q}}$, which is equal to the ratio of the local buoyancy Reynolds number
${\mathcal{Q}}$, which is equal to the ratio of the local buoyancy Reynolds number 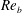 $Re_{b}$ and the friction Reynolds number
$Re_{b}$ and the friction Reynolds number 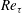 $Re_{\unicode[STIX]{x1D70F}}$. Close to the top and bottom boundaries turbulence is also affected by
$Re_{\unicode[STIX]{x1D70F}}$. Close to the top and bottom boundaries turbulence is also affected by 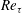 $Re_{\unicode[STIX]{x1D70F}}$ and vertical position
$Re_{\unicode[STIX]{x1D70F}}$ and vertical position  $z$. In the initial heated equilibrium state the laminar surface layer is stabilised by the heat source, which acts as a potential energy sink. Removal of the heat source allows Kelvin–Helmholtz-like shear instabilities to form that lead to a rapid transition to turbulence and significantly enhance the mixing process. The destratifying flow is found to be governed by bulk parameters
$z$. In the initial heated equilibrium state the laminar surface layer is stabilised by the heat source, which acts as a potential energy sink. Removal of the heat source allows Kelvin–Helmholtz-like shear instabilities to form that lead to a rapid transition to turbulence and significantly enhance the mixing process. The destratifying flow is found to be governed by bulk parameters 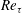 $Re_{\unicode[STIX]{x1D70F}}$,
$Re_{\unicode[STIX]{x1D70F}}$, 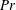 $Pr$ and the friction Richardson number
$Pr$ and the friction Richardson number 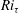 $Ri_{\unicode[STIX]{x1D70F}}$. The overall destratification rate
$Ri_{\unicode[STIX]{x1D70F}}$. The overall destratification rate 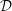 ${\mathcal{D}}$ is found to be a function of
${\mathcal{D}}$ is found to be a function of 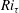 $Ri_{\unicode[STIX]{x1D70F}}$ and
$Ri_{\unicode[STIX]{x1D70F}}$ and 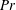 $Pr$.
$Pr$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 18
- Cited by

