Article contents
Evolution of elliptic synthetic jets at low Reynolds number
Published online by Cambridge University Press: 08 April 2019
Abstract
The influence of the nozzle aspect ratio (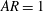 $AR=1$, 2 and 4), stroke length (
$AR=1$, 2 and 4), stroke length (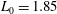 $L_{0}=1.85$, 3.7 and 5.55) and Reynolds number (
$L_{0}=1.85$, 3.7 and 5.55) and Reynolds number (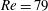 $Re=79$, 158, 316 and 632) on the behaviour of elliptic synthetic jets is studied experimentally. Laser-induced fluorescence and two-dimensional and stereoscopic particle image velocimetry are used to analyse the vortex dynamics and evolution mechanism. It is found that the fluid elements around the major axis of an elliptic vortex ring move downstream faster and tend to approach the centreline, while the fluid elements around the minor axis move downstream at a slower speed and away from the centreline, thereby resulting in the occurrence of the well-known axis-switching phenomenon for elliptic synthetic jets. During this process, a pair of arc-like vortices forms ahead of the primary vortex ring, and they are constituted by streamwise vortices in the leg part and spanwise vortices in the head part; two pairs of streamwise vortices form from the inside of the primary vortex ring and develop in the tails. The streamwise vortices are pushed away progressively from the centreline by the synthetic jet vortex rings that are formed during the subsequent periods. These additional vortical structures for non-circular synthetic jets show regular and periodic characteristics, which are quite different from the previous findings for non-circular jets. Their mutual interaction with the vortex ring causes significant changes in the topology of elliptic synthetic jets, which further results in the variation of the statistical characteristics. Increasing the aspect ratio, stroke length and Reynolds number will make the evolution of the synthetic jet become more unstable and complex. In addition, the entrainment rate of an elliptical synthetic jet is larger than that of a circular synthetic jet and it increases with the nozzle aspect ratio (
$Re=79$, 158, 316 and 632) on the behaviour of elliptic synthetic jets is studied experimentally. Laser-induced fluorescence and two-dimensional and stereoscopic particle image velocimetry are used to analyse the vortex dynamics and evolution mechanism. It is found that the fluid elements around the major axis of an elliptic vortex ring move downstream faster and tend to approach the centreline, while the fluid elements around the minor axis move downstream at a slower speed and away from the centreline, thereby resulting in the occurrence of the well-known axis-switching phenomenon for elliptic synthetic jets. During this process, a pair of arc-like vortices forms ahead of the primary vortex ring, and they are constituted by streamwise vortices in the leg part and spanwise vortices in the head part; two pairs of streamwise vortices form from the inside of the primary vortex ring and develop in the tails. The streamwise vortices are pushed away progressively from the centreline by the synthetic jet vortex rings that are formed during the subsequent periods. These additional vortical structures for non-circular synthetic jets show regular and periodic characteristics, which are quite different from the previous findings for non-circular jets. Their mutual interaction with the vortex ring causes significant changes in the topology of elliptic synthetic jets, which further results in the variation of the statistical characteristics. Increasing the aspect ratio, stroke length and Reynolds number will make the evolution of the synthetic jet become more unstable and complex. In addition, the entrainment rate of an elliptical synthetic jet is larger than that of a circular synthetic jet and it increases with the nozzle aspect ratio (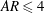 $AR\leqslant 4$) and Reynolds number. It is indicated that the formation of streamwise vortices could enhance the entrainment rate. This finding provides substantial evidence for the potential application of elliptic synthetic jets for effective flow control.
$AR\leqslant 4$) and Reynolds number. It is indicated that the formation of streamwise vortices could enhance the entrainment rate. This finding provides substantial evidence for the potential application of elliptic synthetic jets for effective flow control.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 24
- Cited by

