Article contents
Evolution of a shock generated by an impulsively accelerated, sinusoidal piston
Published online by Cambridge University Press: 26 November 2020
Abstract
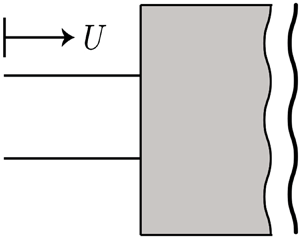
We consider the evolution of a shock wave generated by an impulsively accelerated, two-dimensional, almost planar piston with a sinusoidally corrugated surface of amplitude  $\epsilon$. We develop a complex-variable formulation for a nonlinear theory of generalized geometrical shock dynamics (GGSD) (Best, Shock Waves, vol. 1, issue 4, 1991, pp. 251–273; Best, Proc. R. Soc. Lond. A, vol. 442, 1993, pp. 585–598) as a hierarchical expansion of the Euler equations that can be closed at any order. The zeroth-order truncation of GGSD is related to the equations of Whitham's geometrical shock dynamics (GSD), while higher-order corrections incorporate non-uniformity of the flow immediately behind the piston-driven shock. Numerical solutions to GGSD systems up to second order are coupled to an edge-detection algorithm in order to investigate the hypothesized development of a shock-shape curvature singularity as the rippled shock evolves. This singular behaviour, together with the simultaneous development of a Mach-number discontinuity, is found at all orders of the GGSD hierarchy for both weak and strong shocks. The critical time at which a curvature singularity occurs converges as the order of the GGSD system increases at fixed
$\epsilon$. We develop a complex-variable formulation for a nonlinear theory of generalized geometrical shock dynamics (GGSD) (Best, Shock Waves, vol. 1, issue 4, 1991, pp. 251–273; Best, Proc. R. Soc. Lond. A, vol. 442, 1993, pp. 585–598) as a hierarchical expansion of the Euler equations that can be closed at any order. The zeroth-order truncation of GGSD is related to the equations of Whitham's geometrical shock dynamics (GSD), while higher-order corrections incorporate non-uniformity of the flow immediately behind the piston-driven shock. Numerical solutions to GGSD systems up to second order are coupled to an edge-detection algorithm in order to investigate the hypothesized development of a shock-shape curvature singularity as the rippled shock evolves. This singular behaviour, together with the simultaneous development of a Mach-number discontinuity, is found at all orders of the GGSD hierarchy for both weak and strong shocks. The critical time at which a curvature singularity occurs converges as the order of the GGSD system increases at fixed  $\epsilon$, and follows a scaling inversely proportional to
$\epsilon$, and follows a scaling inversely proportional to  $\epsilon$ at sufficiently small values. This result agrees with the weakly nonlinear GSD analysis of Mostert et al. (J. Fluid Mech., vol. 846, 2018, pp. 536–562) for a general Mach-number perturbation on a planar shock, and suggests that this represents the universal behaviour of a slightly perturbed, planar shock.
$\epsilon$ at sufficiently small values. This result agrees with the weakly nonlinear GSD analysis of Mostert et al. (J. Fluid Mech., vol. 846, 2018, pp. 536–562) for a general Mach-number perturbation on a planar shock, and suggests that this represents the universal behaviour of a slightly perturbed, planar shock.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by


