Article contents
Entrainment of short-wavelength free-stream vortical disturbances in compressible and incompressible boundary layers
Published online by Cambridge University Press: 24 May 2016
Abstract
The fundamental difference between continuous modes of the Orr–Sommerfeld/Squire equations and the entrainment of free-stream vortical disturbances (FSVD) into the boundary layer has been investigated in a recent paper (Dong & Wu, J. Fluid Mech., vol. 732, 2013, pp. 616–659). It was shown there that the non-parallel-flow effect plays a leading-order role in the entrainment, and neglecting it at the outset, as is done in the continuous-mode formulation, leads to non-physical features of ‘Fourier entanglement’ and abnormal anisotropy. The analysis, which was for incompressible boundary layers and for FSVD with a characteristic wavelength of the order of the local boundary-layer thickness, is extended in this paper to compressible boundary layers and FSVD with even shorter wavelengths, which are comparable with the width of the so-called edge layer. Non-parallelism remains a leading-order effect in the present scaling, which turns out to be more general in that the equations and solutions in the previous paper are recovered in the appropriate limit. Appropriate asymptotic solutions in the main and edge layers are obtained to characterize the entrainment. It is found that when the Prandtl number 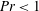 $\mathit{Pr}<1$ , free-stream vortical disturbances of relatively low frequency generate very strong temperature fluctuations within the edge layer, leading to formation of thermal streaks. A composite solution, uniformly valid across the entire boundary layer, is constructed, and it can be used in receptivity studies and as inlet conditions for direct numerical simulations of bypass transition. For compressible boundary layers, continuous spectra of the disturbance equations linearized about a parallel base flow exhibit entanglement between vortical and entropy modes, namely, a vortical mode necessarily induces an entropy disturbance in the free stream and vice versa, and this amounts to a further non-physical behaviour. High Reynolds number asymptotic analysis yields the relations between the amplitudes of entangled modes.
$\mathit{Pr}<1$ , free-stream vortical disturbances of relatively low frequency generate very strong temperature fluctuations within the edge layer, leading to formation of thermal streaks. A composite solution, uniformly valid across the entire boundary layer, is constructed, and it can be used in receptivity studies and as inlet conditions for direct numerical simulations of bypass transition. For compressible boundary layers, continuous spectra of the disturbance equations linearized about a parallel base flow exhibit entanglement between vortical and entropy modes, namely, a vortical mode necessarily induces an entropy disturbance in the free stream and vice versa, and this amounts to a further non-physical behaviour. High Reynolds number asymptotic analysis yields the relations between the amplitudes of entangled modes.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 26
- Cited by


