Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mahmud, Hasan
Lin, Wenxian
Gao, Wenfeng
Armfield, S.W.
and
He, Yinghe
2016.
Interaction behavior of triple transitional round fountains in a homogeneous fluid.
International Journal of Heat and Fluid Flow,
Vol. 62,
Issue. ,
p.
437.
Hunt, Gary R.
and
Debugne, Antoine L. R.
2016.
Forced fountains.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
437.
Herault, J.
Duval, F.
and
Le Bars, M.
2017.
Mass transport induced by a jet impinging on a density interface: The role of interfacial wave breaking.
EPL (Europhysics Letters),
Vol. 117,
Issue. 6,
p.
64003.
Gao, Wenfeng
Lin, Wenxian
Liu, Tao
Armfield, S.W.
and
Li, Ming
2017.
Penetration height of transitional round fountains in a linearly stratified fluid.
International Communications in Heat and Mass Transfer,
Vol. 81,
Issue. ,
p.
79.
Bondur, Valerii G.
Troitskaya, Yuliya I.
Ezhova, Ekaterina V.
Kazakov, Vasiliy I.
Kandaurov, Alexandr A.
Sergeev, Daniil A.
and
Soustova, Irina A.
2018.
The Ocean in Motion.
p.
67.
Lippert, Martin C.
and
Woods, Andrew W.
2018.
Particle fountains in a confined environment.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
28.
Xiao, Canbo
Fan, Wei
Yao, Zhongzhi
Qiang, Yongfa
Pan, Yiwen
and
Chen, Ying
2019.
On the total entrained flow rate of artificial downwelling.
Ocean Engineering,
Vol. 181,
Issue. ,
p.
13.
Xue, Nan
Khodaparast, Sepideh
and
Stone, Howard A.
2019.
Fountain mixing in a filling box at low Reynolds numbers.
Physical Review Fluids,
Vol. 4,
Issue. 2,
McConnochie, Craig D.
Cenedese, Claudia
and
McElwaine, Jim N.
2020.
Surface Expression of a Wall Fountain: Application to Subglacial Discharge Plumes.
Journal of Physical Oceanography,
Vol. 50,
Issue. 5,
p.
1245.
Lippert, Martin C.
and
Woods, Andrew W.
2020.
Experiments on the sedimentation front in steady particle-driven gravity currents.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Mehaddi, R.
Boulet, P.
Koutaiba, M.
Vauquelin, O.
and
Candelier, F.
2021.
Emptying-filling boxes with non-Boussinesq plumes and fountains.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Milton-McGurk, L.
Williamson, N.
Armfield, S.W.
Kirkpatrick, M.P.
and
Talluru, K.M.
2021.
Entrainment and structure of negatively buoyant jets.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Newland, Eric L.
Mingotti, Nicola
and
Woods, Andrew W.
2022.
Dynamics of deep-submarine volcanic eruptions.
Scientific Reports,
Vol. 12,
Issue. 1,
Inam, M. I.
Lin, Wenxian
and
Armfield, S. W.
2022.
Thermal Entrainment in the Core Regions of Transitional Plane Fountains in Linearly Stratified Ambient Fluids.
International Journal of Applied Mechanics,
Vol. 14,
Issue. 03,
Milton-McGurk, L.
Williamson, N.
Armfield, S.W.
and
Kirkpatrick, M.P.
2022.
Characterising entrainment in fountains and negatively buoyant jets.
Journal of Fluid Mechanics,
Vol. 939,
Issue. ,
Talluru, K.M.
Williamson, N.
and
Armfield, S.W.
2022.
Entrainment and dilution in a fountain top.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Huang, Jingzi
Burridge, Henry C.
and
van Reeuwijk, Maarten
2023.
The internal structure of forced fountains.
Journal of Fluid Mechanics,
Vol. 961,
Issue. ,
Xia, Yaowen
and
Chen, Juan
2023.
Experimental investigation of fountains in homogeneous fluid with coexistent temperature and concentration effects using PIV/PLIF.
AIP Advances,
Vol. 13,
Issue. 1,
Vouriot, Carolanne V.M.
van Reeuwijk, Maarten
and
Burridge, Henry C.
2024.
Robustness of point measurements of carbon dioxide concentration for the inference of ventilation rates in a wintertime classroom.
Indoor Environments,
Vol. 1,
Issue. 1,
p.
100004.
Hassanzadeh, H.
and
Taghavi, S. M.
2024.
A review on free miscible buoyant jets.
Physics of Fluids,
Vol. 36,
Issue. 6,
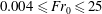 $0.004\leqslant \mathit{Fr}_{0}\leqslant 25$ ) and thereby encompass the entrainment across all classes of fountain behaviour identified to date. We identify scalings for the entrained volume flux
$0.004\leqslant \mathit{Fr}_{0}\leqslant 25$ ) and thereby encompass the entrainment across all classes of fountain behaviour identified to date. We identify scalings for the entrained volume flux 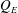 $Q_{E}$ , in terms of
$Q_{E}$ , in terms of 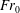 $\mathit{Fr}_{0}$ and the source volume flux
$\mathit{Fr}_{0}$ and the source volume flux 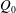 $Q_{0}$ , within a number of distinct Froude-number bands corresponding to each class of fountain. Additionally we identify a distinct class of new behaviour, as yet unreported, for
$Q_{0}$ , within a number of distinct Froude-number bands corresponding to each class of fountain. Additionally we identify a distinct class of new behaviour, as yet unreported, for 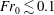 $\mathit{Fr}_{0}\lesssim 0.1$ .
$\mathit{Fr}_{0}\lesssim 0.1$ .

