No CrossRef data available.
Article contents
Enhancing large-scale motions and turbulent transport in rotating plane Poiseuille flow
Published online by Cambridge University Press: 22 January 2024
Abstract
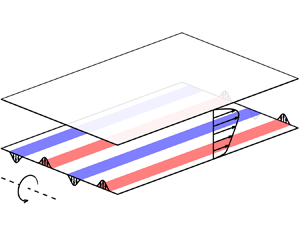
Based on the characteristics of large-scale plume currents in rotating plane Poiseuille flows (RPPF), an injection/suction control strategy is introduced to augment the intensity of plume currents and improve the turbulent transport of passive scalar. The control strategy maintains the conventional non-penetrative condition on the stable side, and applies a wall-normal velocity that varies in the spanwise direction on the unstable side. For comparison, the control with non-penetrative condition on the unstable side and injection/suction on the stable side is also examined. The RPPF at  $Re_\tau$ ranging from
$Re_\tau$ ranging from  $180$ to
$180$ to  $300$ and
$300$ and  $Ro_\tau$ ranging from
$Ro_\tau$ ranging from  $0$ to
$0$ to  $30$ are studied. Injection/suction with fixed root-mean-squared wall-normal velocity (below
$30$ are studied. Injection/suction with fixed root-mean-squared wall-normal velocity (below  $1\,\%$ of the bulk mean velocity) at the wall is considered. Direct numerical simulations reveal that the injection/suction on the stable side has minor effect for all cases studied, whereas the injection/suction with properly distributed slots on the unstable side can significantly enhance the large-scale plume currents and the turbulent transport efficiency at small or moderate rotation numbers. This is attributed to the fact that plumes are generated on the unstable side, and controlling the origin of plumes is more effective. A proper strategy for maximum enhancement of turbulent transport is limiting the distance between injection slots equal to or slightly larger than the intrinsic distance between plume currents. This strategy is valid for all physical and computational parameters currently considered, and is potentially applicable over a much wider parameter range.
$1\,\%$ of the bulk mean velocity) at the wall is considered. Direct numerical simulations reveal that the injection/suction on the stable side has minor effect for all cases studied, whereas the injection/suction with properly distributed slots on the unstable side can significantly enhance the large-scale plume currents and the turbulent transport efficiency at small or moderate rotation numbers. This is attributed to the fact that plumes are generated on the unstable side, and controlling the origin of plumes is more effective. A proper strategy for maximum enhancement of turbulent transport is limiting the distance between injection slots equal to or slightly larger than the intrinsic distance between plume currents. This strategy is valid for all physical and computational parameters currently considered, and is potentially applicable over a much wider parameter range.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


