Article contents
Enhanced velocity fluctuations in interacting swimmer suspensions
Published online by Cambridge University Press: 25 November 2020
Abstract
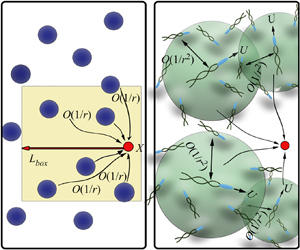
This paper characterizes the nature of velocity fluctuations in swimmer suspensions by determining the fluid velocity variance and the diffusivity of immersed passive tracers in dilute suspensions of hydrodynamically interacting slender microswimmers. The swimmers considered include straight-swimmers whose orientations change only on account of hydrodynamic interactions, and run-and-tumble particles (RTPs) whose orientations change in addition due to tumble events obeying Poisson statistics. In a dilute non-interacting swimmer suspension, the fluid velocity variance is finite and the covariance is short ranged, decaying for distances larger than the swimmer length. In contrast, we show, for a suspension of interacting straight-swimmers, that pair interactions lead to a non-decaying velocity covariance, and a variance that diverges logarithmically with system size. For suspensions of RTPs, the aforementioned divergence is arrested due to tumbling. While the variance remains finite, and the covariance short ranged, for suspensions of interacting rapid tumbling RTPs (short run lengths), the underlying straight-swimmer divergence manifests as a logarithmic increase of the variance with the swimmer run length for persistent RTPs (long run lengths), with a correspondingly long-ranged covariance. The tracer mean squared displacement undergoes an increasingly broad crossover from the ballistic to the diffusive regime for persistent RTPs, with the tracer diffusivity exhibiting a stronger linear increase with the swimmer run length. Our analysis explains the bifurcation of the velocity variance and tracer diffusivities between pusher and puller suspensions, as well as numerous observations of a volume-fraction-dependent crossover time for passive tracer dynamics.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Present address: Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm 10691, Sweden.
References
REFERENCES
- 6
- Cited by


