Article contents
Electrokinetics at liquid/liquid interfaces
Published online by Cambridge University Press: 28 September 2011
Abstract
Electrokinetic effects at liquid/liquid interfaces have received considerably less attention than at solid/liquid interfaces. Because liquid/liquid interfaces are generally mobile, one might expect electrokinetic effects over a liquid/liquid interface to be faster than over an equivalent solid surface. The earliest predictions for the electrophoretic mobility of charged mercury drops – distinct approaches by Frumkin, along with Levich, and Booth – differed by 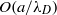 , where
, where  is the radius of the drop and
is the radius of the drop and 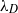 is the Debye length. Seeking to reconcile this rather striking discrepancy, Levine & O’Brien showed double-layer polarization to be the key ingredient. Without a physical mechanism by which electrokinetic effects are enhanced, however, it is difficult to know how general the enhancement is – whether it holds only for liquid metal surfaces, or more generally, for all liquid/liquid surfaces. By considering a series of systems in which a planar metal strip is coated with either a liquid metal or liquid dielectric, we show that the central physical mechanism behind the enhancement predicted by Frumkin is the presence of an unmatched electrical stress upon the electrolyte/liquid interface, which establishes a Marangoni stress on the droplet surface and drives it into motion. The source of the unbalanced electrokinetic stress on a liquid metal surface is clear – metals represent equipotential surfaces, so no field exists to drive an equal and opposite force on the surface charge. This might suggest that liquid metals represent a unique system, since dielectric liquids can support finite electric fields, which might be expected to exert an electrical stress on the surface charge that balances the electric stress. We demonstrate, however, that electrical and osmotic stresses on relaxed double layers internal to dielectric liquids precisely cancel, so that internal electrokinetic stresses generally vanish in closed, ideally polarizable liquids. The enhancement predicted by Frumkin for liquid mercury drops can thus be expected quite generally over ideally polarizable liquid drops. We then reconsider the electrophoretic mobility of spherical drops, and reconcile the approaches of Frumkin and Booth: Booth’s neglect of double-layer polarization leads to a standard electro-osmotic flow, without the enhancement, and Frumkin’s neglect of the detailed double-layer dynamics leads to the enhanced electrocapillary motion, but does not capture the (sub-dominant) electrophoretic motion. Finally, we show that, while the electrokinetic flow over electrodes coated with thin liquid films is
is the Debye length. Seeking to reconcile this rather striking discrepancy, Levine & O’Brien showed double-layer polarization to be the key ingredient. Without a physical mechanism by which electrokinetic effects are enhanced, however, it is difficult to know how general the enhancement is – whether it holds only for liquid metal surfaces, or more generally, for all liquid/liquid surfaces. By considering a series of systems in which a planar metal strip is coated with either a liquid metal or liquid dielectric, we show that the central physical mechanism behind the enhancement predicted by Frumkin is the presence of an unmatched electrical stress upon the electrolyte/liquid interface, which establishes a Marangoni stress on the droplet surface and drives it into motion. The source of the unbalanced electrokinetic stress on a liquid metal surface is clear – metals represent equipotential surfaces, so no field exists to drive an equal and opposite force on the surface charge. This might suggest that liquid metals represent a unique system, since dielectric liquids can support finite electric fields, which might be expected to exert an electrical stress on the surface charge that balances the electric stress. We demonstrate, however, that electrical and osmotic stresses on relaxed double layers internal to dielectric liquids precisely cancel, so that internal electrokinetic stresses generally vanish in closed, ideally polarizable liquids. The enhancement predicted by Frumkin for liquid mercury drops can thus be expected quite generally over ideally polarizable liquid drops. We then reconsider the electrophoretic mobility of spherical drops, and reconcile the approaches of Frumkin and Booth: Booth’s neglect of double-layer polarization leads to a standard electro-osmotic flow, without the enhancement, and Frumkin’s neglect of the detailed double-layer dynamics leads to the enhanced electrocapillary motion, but does not capture the (sub-dominant) electrophoretic motion. Finally, we show that, while the electrokinetic flow over electrodes coated with thin liquid films is 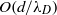 faster than over solid/liquid interfaces, the Dukhin number,
faster than over solid/liquid interfaces, the Dukhin number,  , which reflects the importance of surface conduction to bulk conduction, generally increases by a smaller amount [
, which reflects the importance of surface conduction to bulk conduction, generally increases by a smaller amount [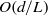 ], where
], where 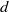 is the thickness of film and
is the thickness of film and 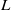 is the length of the electrode. This suggests that liquid/liquid interfaces may be utilized to enhance electrokinetic velocities in microfluidic devices, while delaying the onset of high-
is the length of the electrode. This suggests that liquid/liquid interfaces may be utilized to enhance electrokinetic velocities in microfluidic devices, while delaying the onset of high-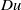 electrokinetic suppression.
electrokinetic suppression.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 33
- Cited by

