Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dixit, Harish N.
and
Homsy, G. M.
2013.
The elastocapillary Landau–Levich problem.
Journal of Fluid Mechanics,
Vol. 735,
Issue. ,
p.
1.
Jung, Yoon Dong
and
Ahn, Kyung Hyun
2013.
Prediction of Coating Thickness in the Convective Assembly Process.
Langmuir,
Vol. 29,
Issue. 51,
p.
15762.
Trinh, Philippe H.
Wilson, Stephen K.
and
Stone, Howard A.
2014.
A pinned or free-floating rigid plate on a thin viscous film.
Journal of Fluid Mechanics,
Vol. 760,
Issue. ,
p.
407.
McHale, G.
and
Newton, M. I.
2015.
Liquid marbles: topical context within soft matter and recent progress.
Soft Matter,
Vol. 11,
Issue. 13,
p.
2530.
Li, Xue
and
Gilchrist, James F.
2016.
Large-Area Nanoparticle Films by Continuous Automated Langmuir–Blodgett Assembly and Deposition.
Langmuir,
Vol. 32,
Issue. 5,
p.
1220.
Rio, Emmanuelle
and
Boulogne, François
2017.
Withdrawing a solid from a bath: How much liquid is coated?.
Advances in Colloid and Interface Science,
Vol. 247,
Issue. ,
p.
100.
Kim, Onyu
and
Nam, Jaewook
2017.
Confinement effects in dip coating.
Journal of Fluid Mechanics,
Vol. 827,
Issue. ,
p.
1.
Morozov, Matvey
and
Manor, Ofer
2017.
An extended Landau–Levich model for the dragging of a thin liquid film with a propagating surface acoustic wave.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
307.
Galindo, Sergi
Tamayo, Adrián
Leonardi, Francesca
and
Mas‐Torrent, Marta
2017.
Control of Polymorphism and Morphology in Solution Sheared Organic Field‐Effect Transistors.
Advanced Functional Materials,
Vol. 27,
Issue. 25,
Kusaka, Yasuyuki
Manaka, Sakae
Abe, Koji
Yamamoto, Noritaka
and
Ushijima, Hirobumi
2017.
Experimental study on injecting highly viscous liquids by using a reciprocating needle dispensing system.
The International Journal of Advanced Manufacturing Technology,
Vol. 90,
Issue. 5-8,
p.
2243.
Riera-Galindo, Sergi
Tamayo, Adrián
and
Mas-Torrent, Marta
2018.
Role of Polymorphism and Thin-Film Morphology in Organic Semiconductors Processed by Solution Shearing.
ACS Omega,
Vol. 3,
Issue. 2,
p.
2329.
Pihler-Puzović, Draga
Peng, Gunnar G.
Lister, John R.
Heil, Matthias
and
Juel, Anne
2018.
Viscous fingering in a radial elastic-walled Hele-Shaw cell.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
163.
Barakat, Joseph M.
and
Shaqfeh, Eric S. G.
2018.
The steady motion of a closely fitting vesicle in a tube.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
721.
Wang, Kaishi
Bordia, Rajendra K.
and
Brush, Lucien N.
2019.
A semi-empirical power-law model for the dip-coating of a substrate into a particle-containing, non-Newtonian, complex fluid system.
Ceramics International,
Vol. 45,
Issue. 6,
p.
6655.
Krapez, Marion
Gauthier, Anaïs
Kellay, Hamid
Boitte, Jean-Baptiste
Aubrun, Odile
Joanny, Jean-François
and
Colin, Annie
2020.
Impact of the Wetting Length on Flexible Blade Spreading.
Physical Review Letters,
Vol. 125,
Issue. 25,
Warburton, Katarzyna L. P.
Hewitt, Duncan R.
and
Neufeld, Jerome A.
2020.
The elastic Landau–Levich problem on a slope.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Choudhury, Anjishnu
Paidi, Venkatesh Kumar
Kalpathy, Sreeram K.
and
Dixit, Harish N.
2020.
Enhanced stability of free viscous films due to surface viscosity.
Physics of Fluids,
Vol. 32,
Issue. 8,
Champougny, Lorène
Scheid, Benoit
Korobkin, Alexander A.
and
Rodríguez-Rodríguez, Javier
2021.
Dip-coating flow in the presence of two immiscible liquids.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Chan, Tak Shing
Pedersen, Christian
Koplik, Joel
and
Carlson, Andreas
2021.
Film deposition and dynamics of a self-propelled wetting droplet on a conical fibre.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Wang, Zhi-Qiao
and
Detournay, Emmanuel
2021.
Force on a moving liquid blister.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
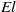 $\mathit{El}$ , which represents the relative strength of viscous forces to elasticity. The main assumptions of the theory are that
$\mathit{El}$ , which represents the relative strength of viscous forces to elasticity. The main assumptions of the theory are that 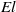 $\mathit{El}$ be small, and that surface tension effects are negligible. The shape of the free surface is formulated as a nonlinear boundary value problem: we develop the solution as an asymptotic expansion in the small parameter
$\mathit{El}$ be small, and that surface tension effects are negligible. The shape of the free surface is formulated as a nonlinear boundary value problem: we develop the solution as an asymptotic expansion in the small parameter 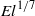 ${\mathit{El}}^{1/ 7} $ and use the method of matched asymptotic expansions to determine the film thickness as a function of
${\mathit{El}}^{1/ 7} $ and use the method of matched asymptotic expansions to determine the film thickness as a function of 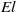 $\mathit{El}$ . The solution to the shape of the static meniscus is not as straightforward as in the classical Landau–Levich problem, as evaluation of higher-order effects is necessary in order to close the problem. A remarkable aspect of the problem is the occurrence of multiple solutions, and five of these are found numerically. In any event, the film thickness varies as
$\mathit{El}$ . The solution to the shape of the static meniscus is not as straightforward as in the classical Landau–Levich problem, as evaluation of higher-order effects is necessary in order to close the problem. A remarkable aspect of the problem is the occurrence of multiple solutions, and five of these are found numerically. In any event, the film thickness varies as 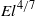 ${\mathit{El}}^{4/ 7} $ in qualitative agreement with the experiments of Ouriemi & Homsy (Phys. Fluids, 2013, in press).
${\mathit{El}}^{4/ 7} $ in qualitative agreement with the experiments of Ouriemi & Homsy (Phys. Fluids, 2013, in press).
