Article contents
Eigenvalue sensitivity, singular values and discrete frequency selection mechanism in noise amplifiers: the case of flow induced by radial wall injection
Published online by Cambridge University Press: 26 September 2014
Abstract
We have performed linearized direct numerical simulations (DNS) of flow induced by radial wall injection forced by white-noise Gaussian forcings. We have shown that the frequency spectrum of the flow exhibits low-frequency discrete peaks in the case of a spatial structure of the forcing that is large scale. On the other hand, we observed that the spectrum becomes smooth (with no discrete peaks) if the spatial structure of the forcing is of a smaller extent. We have then tried to analyse these results in the light of global stability analyses. We have first computed the eigenvalue spectrum of the Jacobian and shown that the computed eigenvalues in the frequency range of interest were strongly damped and extremely sensitive to numerical discretization choices if large domains in the axial direction were considered. If shorter domains are used, then the eigenvalues are more robust but still extremely sensitive to the location of the upstream and downstream boundaries. Analysis of the  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\epsilon $ -pseudo-spectrum showed that eigenvalues located in a region displaying ‘background’ values of
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\epsilon $ -pseudo-spectrum showed that eigenvalues located in a region displaying ‘background’ values of  $ \epsilon $ below
$ \epsilon $ below 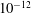 $10^{-12}$ were extremely sensitive and confirmed that all values in this region of the spectrum were actually quasi-eigenvalues. The eigenvalues are therefore ill-behaved and cannot be invoked to explain the observed discrete frequency selection mechanism. We have then performed a singular value decomposition of the global resolvent matrix to compute the leading optimal gains, optimal forcings and optimal responses, which are robust quantities, insensitive to numerical discretization details. We showed that the frequency response of the flow with the large-scale forcing can accurately be reproduced by an approximation based on the leading optimal gain/forcing/response. Analysis of this approximation showed that it is the projection coefficient of the forcing onto the leading optimal forcing that is responsible for the discrete frequency selection mechanism in the case of the large-scale forcing. From a more physical point of view, such a discrete behaviour stems from the streamwise oscillations of the leading optimal forcings, whose wavelengths vary with frequency, in combination with finite extent forcings (which start or end at locations where the leading optimal forcings are strong). Experimental results in the literature are finally discussed in light of these findings.
$10^{-12}$ were extremely sensitive and confirmed that all values in this region of the spectrum were actually quasi-eigenvalues. The eigenvalues are therefore ill-behaved and cannot be invoked to explain the observed discrete frequency selection mechanism. We have then performed a singular value decomposition of the global resolvent matrix to compute the leading optimal gains, optimal forcings and optimal responses, which are robust quantities, insensitive to numerical discretization details. We showed that the frequency response of the flow with the large-scale forcing can accurately be reproduced by an approximation based on the leading optimal gain/forcing/response. Analysis of this approximation showed that it is the projection coefficient of the forcing onto the leading optimal forcing that is responsible for the discrete frequency selection mechanism in the case of the large-scale forcing. From a more physical point of view, such a discrete behaviour stems from the streamwise oscillations of the leading optimal forcings, whose wavelengths vary with frequency, in combination with finite extent forcings (which start or end at locations where the leading optimal forcings are strong). Experimental results in the literature are finally discussed in light of these findings.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 9
- Cited by

