No CrossRef data available.
Article contents
The effective shear and dilatational viscosities of a particle-laden interface in the dilute limit
Published online by Cambridge University Press: 28 September 2020
Abstract
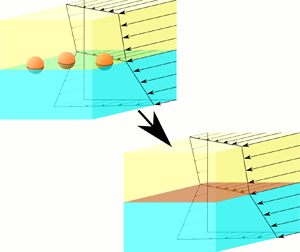
The effective dilatational and shear viscosities of a particle-laden fluid interface are computed in the dilute limit under the assumption of an asymptotically vanishing viscosity ratio between the two fluids. Spherical particles with a given contact angle of the fluid interface at the particle surface are considered. A planar fluid interface and a small Reynolds number are assumed. The theoretical analysis is based on a domain perturbation expansion in the deviation of the contact angle from  $90^{\circ }$ up to the second order. The resulting effective dilatational viscosity shows a stronger dependence on the contact angle than the effective shear viscosity, and its magnitude is larger for all contact angles. The limits of validity of the theory are discussed.
$90^{\circ }$ up to the second order. The resulting effective dilatational viscosity shows a stronger dependence on the contact angle than the effective shear viscosity, and its magnitude is larger for all contact angles. The limits of validity of the theory are discussed.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press


