Article contents
Effect of free surface on submerged stratified shear instabilities
Published online by Cambridge University Press: 19 March 2018
Abstract
In this paper, we have considered the effects of the shallowness of the domain as well as the air–water free surface on the stratified shear instabilities of the fluid underneath. First, we numerically solve the non-Boussinesq Taylor–Goldstein equation for smooth velocity and density profiles of a model shear layer with a free surface. When the depth of the fluid is relatively shallow compared to the shear layer thickness, the surface gravity waves existing at the free surface come closer to the waves existing in the shear layer. This can lead to resonant wave interactions, making the flow unstable to more varieties of modal instabilities. In order to obtain a deeper understanding of the instability mechanisms, we have performed analytical studies with broken-line profiles (profiles for which vorticity and density are piecewise constant). Furthermore, reduced-order broken-line profiles have also been developed, based on which dispersion diagrams are constructed. Through these diagrams we have underpinned the resonantly interacting waves leading to each type of instability. Two new instabilities have been found; one of them, referred to as the ‘surface gravity – interfacial gravity (SG-IG) mode’, arises due to the interaction between a surface gravity wave and an interfacial gravity wave, and would therefore be absent if there is no internal density stratification. The other one – the ‘surface gravity – lower vorticity (SG-LV) mode’, which arises due to the interaction between a surface gravity wave and the lower vorticity wave, surpasses Kelvin–Helmholtz (KH) instability to become the most unstable mode, provided the system is significantly shallow. Stability boundary of the SG-LV mode is found to be quite different from that of KH. In fact, KH becomes negligible for relatively shallow flows, while SG-LV’s growth rate is significant – comparable to the growth rate of KH for unbounded domains (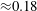 ${\approx}0.18$). Moreover, the SG-LV mode is found to be analogous to the barotropic mode observed in two-layer quiescent flows. We have found that the effect of a free surface on the Holmboe instability is not appreciable. Holmboe in the presence of a free surface is found to be analogous to the baroclinic mode observed in two-layer quiescent flows. Except for the Holmboe instability, remarkable differences are observed in all other instabilities occurring in shallow domains when the air–water interface is replaced by a rigid lid. We infer that the rigid-lid approximation is valid for large vertical domains and should be applied with caution otherwise. Furthermore, we have also shown that if shear is absent at the free surface, our problem can be modelled using Boussinesq approximation, that is,
${\approx}0.18$). Moreover, the SG-LV mode is found to be analogous to the barotropic mode observed in two-layer quiescent flows. We have found that the effect of a free surface on the Holmboe instability is not appreciable. Holmboe in the presence of a free surface is found to be analogous to the baroclinic mode observed in two-layer quiescent flows. Except for the Holmboe instability, remarkable differences are observed in all other instabilities occurring in shallow domains when the air–water interface is replaced by a rigid lid. We infer that the rigid-lid approximation is valid for large vertical domains and should be applied with caution otherwise. Furthermore, we have also shown that if shear is absent at the free surface, our problem can be modelled using Boussinesq approximation, that is, 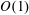 $O(1)$ density variations in the inertial terms can still be neglected.
$O(1)$ density variations in the inertial terms can still be neglected.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331, USA.
References
- 5
- Cited by

