Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fang, Chenyu
Pan, Xuncheng
Zhang, Bo
Zhang, Kuandi
and
Lv, Xiangru
2021.
An experimental study on the evolution law of roll wave parameters in overland flow.
Hydrological Processes,
Vol. 35,
Issue. 11,
Kanellopoulos, Giorgos
2021.
The granular monoclinal wave: a dynamical systems survey.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
de Oliveira Ferreira, Fabiana
Maciel, Geraldo de Freitas
and
Pereira, João Batista
2021.
Roll waves and their generation criteria.
RBRH,
Vol. 26,
Issue. ,
Fei, Jianbo
Jie, Yuxin
Xiong, Hao
and
Wu, Zezhou
2021.
Granular roll waves along a long chute: From formation to collapse.
Powder Technology,
Vol. 377,
Issue. ,
p.
553.
Kanellopoulos, Giorgos
Razis, Dimitrios
and
van der Weele, Ko
2021.
On the structure of granular jumps: the dynamical systems approach.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
Kanellopoulos, Giorgos
Razis, Dimitrios
and
van der Weele, Ko
2022.
On the shape and size of granular roll waves.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Langham, Jake
and
Hogg, Andrew J.
2022.
General linear stability properties of monoclinal shallow waves.
Physical Review Fluids,
Vol. 7,
Issue. 5,
van der Weele, Ko
Razis, Dimitrios
and
Kanellopoulos, Giorgos
2023.
Chaos, Fractals and Complexity.
p.
199.
Razis, Dimitrios
Kanellopoulos, Giorgos
and
van der Weele, Ko
2023.
Roll waves as relaxation oscillations.
Physics of Fluids,
Vol. 35,
Issue. 6,
Guo, Xiaojun
Li, Yong
Yao, Yingjie
Liu, Daochuan
and
Zhang, Jun
2023.
A Pareto–Poisson process model for intermittent debris flow surges developing from slope failures.
Engineering Geology,
Vol. 314,
Issue. ,
p.
106998.
Li, Xingyue
Sovilla, Betty
Gray, John Mark Nicholas Timm
and
Gaume, Johan
2024.
Transient wave activity in snow avalanches is controlled by entrainment and topography.
Communications Earth & Environment,
Vol. 5,
Issue. 1,
Kanellopoulos, Giorgos
2024.
Undular bores in granular suspensions: a dynamical systems study.
Nonlinear Dynamics,
Vol. 112,
Issue. 21,
p.
18977.
da Cunha, Evandro Fernandes
de Oliveira Ferreira, Fabiana
de Freitas Maciel, Geraldo
and
Kitano, Cláudio
2024.
Absorbance photometric technique to measure roll waves in a free surface of a non-Newtonian fluid flow.
Measurement,
Vol. 235,
Issue. ,
p.
114880.
Kanellopoulos, Giorgos
Razis, Dimitrios
and
van der Weele, Ko
2024.
Pairwise balancing of forces in traveling granular waves.
Physica D: Nonlinear Phenomena,
Vol. 469,
Issue. ,
p.
134324.
Kanellopoulos, Giorgos
2024.
Granular roll waves on a
μ
(J) rheology model: A dynamical systems perspective.
Physics of Fluids,
Vol. 36,
Issue. 2,
Kanellopoulos, Giorgos
2025.
Formation of standing waves in granular chute flows induced by mild basal topography.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 343,
Issue. ,
p.
105453.
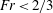 $Fr<2/3$ one finds either a uniform flow of constant thickness or a monoclinal flood wave, i.e. a shock structure monotonically connecting a thick region upstream to a shallower region downstream. For
$Fr<2/3$ one finds either a uniform flow of constant thickness or a monoclinal flood wave, i.e. a shock structure monotonically connecting a thick region upstream to a shallower region downstream. For 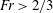 $Fr>2/3$ both the uniform flow and the monoclinal wave cease to be stable; the flow now organizes itself in the form of a train of roll waves. From the governing Saint-Venant equations we derive a dynamical system that elucidates the transition from monoclinal waves to roll waves. It is found that this transition involves several intermediate stages, including an undular bore that had hitherto not been reported for granular flows.
$Fr>2/3$ both the uniform flow and the monoclinal wave cease to be stable; the flow now organizes itself in the form of a train of roll waves. From the governing Saint-Venant equations we derive a dynamical system that elucidates the transition from monoclinal waves to roll waves. It is found that this transition involves several intermediate stages, including an undular bore that had hitherto not been reported for granular flows.
