No CrossRef data available.
Article contents
Dual scaling and the 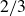 $2/3$ power law for the second-order scalar structure function in homogeneous turbulence with a mean scalar gradient
$2/3$ power law for the second-order scalar structure function in homogeneous turbulence with a mean scalar gradient
Published online by Cambridge University Press: 24 June 2025
Abstract
A dual scaling of the second-order scalar structure function  $\overline {{(\delta \theta )}^2}$, i.e. a scaling based on the Batchelor–Kolmogorov scales
$\overline {{(\delta \theta )}^2}$, i.e. a scaling based on the Batchelor–Kolmogorov scales  $\theta _B$,
$\theta _B$,  $\eta$ and another based on
$\eta$ and another based on  $\theta '$,
$\theta '$,  $L$, representative of the large-scale motion, is examined in the context of the transport equation for
$L$, representative of the large-scale motion, is examined in the context of the transport equation for  $\overline {{(\delta \theta )}^2}$. Direct numerical simulation data over a relatively wide range of the Taylor microscale Reynolds number
$\overline {{(\delta \theta )}^2}$. Direct numerical simulation data over a relatively wide range of the Taylor microscale Reynolds number  $Re_\lambda$ and a Schmidt number of order 1 in statistically stationary homogeneous isotropic turbulence with a uniform mean scalar gradient are used. It is observed that as
$Re_\lambda$ and a Schmidt number of order 1 in statistically stationary homogeneous isotropic turbulence with a uniform mean scalar gradient are used. It is observed that as  $Re_\lambda$ increases, a dual scaling appears to emerge, where the scaling based on
$Re_\lambda$ increases, a dual scaling appears to emerge, where the scaling based on  $\theta '$,
$\theta '$,  $L$ extends to increasingly smaller values of
$L$ extends to increasingly smaller values of  $r/L$, where
$r/L$, where  $r$ is the separation associated with the increment
$r$ is the separation associated with the increment  $ {{\delta \theta }}$, while the scaling based on
$ {{\delta \theta }}$, while the scaling based on  $\theta _B$,
$\theta _B$,  $\eta$ extends to increasingly larger values of
$\eta$ extends to increasingly larger values of  $r/\eta$. This suggests that both scalings should eventually overlap over a range of scales as
$r/\eta$. This suggests that both scalings should eventually overlap over a range of scales as  $Re_\lambda$ continues to increase. Further, it is shown that such a dual scaling leads to the power-law relation
$Re_\lambda$ continues to increase. Further, it is shown that such a dual scaling leads to the power-law relation  $\overline {{(\delta \theta )}^2} \sim r^{\zeta _2}$, where
$\overline {{(\delta \theta )}^2} \sim r^{\zeta _2}$, where  $\zeta _2=2/3$ in the overlap region. The use of an empirical model for the local slope of
$\zeta _2=2/3$ in the overlap region. The use of an empirical model for the local slope of  $\overline {{(\delta \theta )}^2}$ (i.e.
$\overline {{(\delta \theta )}^2}$ (i.e.  $\zeta _2$) shows that a value of
$\zeta _2$) shows that a value of  $Re_\lambda$ of order
$Re_\lambda$ of order  $10^4$ is required for the slope to first reach the value
$10^4$ is required for the slope to first reach the value  $2/3$. Clearly, values larger than
$2/3$. Clearly, values larger than  $10^4$ will be required before a
$10^4$ will be required before a  $r^{2/3}$ inertial range is established.
$r^{2/3}$ inertial range is established.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press


