Article contents
Drying by pervaporation in elementary channel networks
Published online by Cambridge University Press: 09 November 2020
Abstract
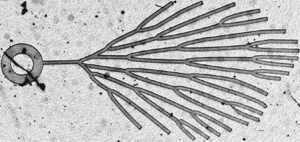
The drying dynamics inside a network of interconnected channels driven by pervaporation, e.g. by diffusion of water through a permeable material surrounding the channels, is studied. The channels are initially filled with water and a single air/water meniscus is initiated at the entrance of the network; drying proceeds as menisci progressively invade the network. The study is focused on elementary networks: simple branched networks without reconnections, or simple loops, in order to get a clear physical picture on which an understanding of drying on more complex networks, such as those encountered in leaves, could be built in the near future. Experiments are compared with models which elaborate on a previously published single-channel model (Dollet et al., J. R. Soc. Interface, vol. 16, 2019, 20180690). In branched networks, experiments reveal velocity discontinuities of the menisci as they split at the nodes. In loops, it is found that the drying rate depends on the number of menisci bounding a given connected water region; when there are two such menisci, a prediction of the dynamics of each of them is proposed, based on the pervaporation-induced hydrodynamics inside the channels. Experiments and model predictions compare favourably for the global drying rate. Some deviations are found for the dynamics of individual menisci, which are ascribed to the sensitivity of the dynamics to small fluctuations in wetting conditions.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


