Published online by Cambridge University Press: 19 February 2019
The primary and secondary laminar flows in annuli with longitudinal grooves and driven by pressure gradients have been analysed. There exist geometric configurations reducing pressure losses in primary flows in spite of an increase of the wall wetted area. The parameter ranges when such flows exist have been determined using linear stability theory. Two types of secondary flows have been identified. The first type has the form of the classical travelling waves driven by shear and modified by the grooves. The axisymmetric waves dominate for sufficiently large radii of the annuli while different spiral waves dominate for small radii. The secondary flow topology is unique in the former case and has the form of axisymmetric rings propagating in the axial direction. Topologies in the latter case are not unique, as spiral waves with left and right twists can emerge under the same conditions, resulting in flow structures varying from spatial rings to rhombic forms. The most intense motion of this type occurs near the walls. The second type of secondary flow has the form of travelling waves driven by inertial effects with characteristics very distinct from the shear waves. Its critical Reynolds number increases proportionally to 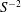 $S^{-2}$, where
$S^{-2}$, where 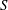 $S$ denotes the groove amplitude, while the amplification rates increase proportionally to
$S$ denotes the groove amplitude, while the amplification rates increase proportionally to 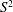 $S^{2}$. These waves exist only if
$S^{2}$. These waves exist only if 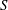 $S$ is above a well-defined minimum and their axisymmetric forms dominate, with the most intense motion occurring near the annulus mid-section. Geometries that give preference to the latter waves have been identified. It is shown that the drag-reducing topographies stabilize the classical travelling waves; these waves are driven by viscous shear, so reduction of this shear decreases their amplification. The same topographies destabilize the new waves; these waves are driven by an inviscid mechanism associated with the formation of circumferential inflection points, and an increase of the groove amplitude increases their amplification. The flow conditions when the presence of grooves can be ignored, i.e. the annuli can be treated as being hydraulically smooth, have been determined.
$S$ is above a well-defined minimum and their axisymmetric forms dominate, with the most intense motion occurring near the annulus mid-section. Geometries that give preference to the latter waves have been identified. It is shown that the drag-reducing topographies stabilize the classical travelling waves; these waves are driven by viscous shear, so reduction of this shear decreases their amplification. The same topographies destabilize the new waves; these waves are driven by an inviscid mechanism associated with the formation of circumferential inflection points, and an increase of the groove amplitude increases their amplification. The flow conditions when the presence of grooves can be ignored, i.e. the annuli can be treated as being hydraulically smooth, have been determined.