Article contents
The drag on a flattened bubble moving across a plane substrate
Published online by Cambridge University Press: 01 March 2012
Abstract
The equilibrium shape of an axisymmetric liquid drop or gas bubble in an immiscible supporting liquid held under gravity against a horizontal plane rigid surface is derived. A thin film of supporting liquid remains between the drop/bubble surface and the rigid substrate at equilibrium, of thickness 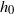 determined by the balance of the disjoining pressure
determined by the balance of the disjoining pressure 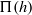 between the drop and the substrate and the internal Laplace pressure of the drop/bubble. The interface is macroscopically flat around the drop axis out to a radius
between the drop and the substrate and the internal Laplace pressure of the drop/bubble. The interface is macroscopically flat around the drop axis out to a radius  but matches smoothly into the outer shape of radius
but matches smoothly into the outer shape of radius 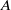 through a boundary layer region of width
through a boundary layer region of width 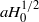 where
where 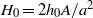 is a small parameter. The outer drop shape is determined by a balance of buoyancy forces and local Laplace pressure and is roughly spherical if
is a small parameter. The outer drop shape is determined by a balance of buoyancy forces and local Laplace pressure and is roughly spherical if 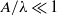 , where
, where 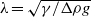 is the capillary length in the interface with a logarithmic correction due to the action of the disjoining pressure across the flattened region. With the shape determined, we calculate the drag force on this flattened bubble to lowest order in the velocity as it moves across the rigid substrate using a lubrication approximation valid to terms of
is the capillary length in the interface with a logarithmic correction due to the action of the disjoining pressure across the flattened region. With the shape determined, we calculate the drag force on this flattened bubble to lowest order in the velocity as it moves across the rigid substrate using a lubrication approximation valid to terms of 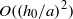 as an integral over the flattened bubble surface of the hydrodynamic pressure. The lubrication theory of itself is not sufficient to determine the drag due to the divergence of that integral if the outer flow field properties are neglected. By using the known exact result for the drag force on an undistorted bubble, the drag on the flattened bubble can be computed as an integral over the lubrication region alone. We derive the drag as a series expansion in the small parameter
as an integral over the flattened bubble surface of the hydrodynamic pressure. The lubrication theory of itself is not sufficient to determine the drag due to the divergence of that integral if the outer flow field properties are neglected. By using the known exact result for the drag force on an undistorted bubble, the drag on the flattened bubble can be computed as an integral over the lubrication region alone. We derive the drag as a series expansion in the small parameter 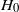 by means of a fairly intricate boundary layer analysis. The logarithmic divergence of the translational drag with film thickness
by means of a fairly intricate boundary layer analysis. The logarithmic divergence of the translational drag with film thickness 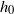 for the undistorted bubble is replaced by the stronger divergence
for the undistorted bubble is replaced by the stronger divergence 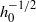 to leading order for the flattened bubble case. We present explicit numerical results for the first few terms in the expansion for the case of an exponentially repulsive disjoining pressure, and analytic expressions for these terms in the limit of very short-range disjoining pressure forces. The results of this calculation are compared with recent work (Hodges, Jensen & Rallison, J. Fluid Mech., vol. 512, 2004, p. 95) where disjoining pressure is neglected and hydrodynamic pressure is balanced against buoyancy and Laplace forces. The limits of validity of this linear drag theory are also presented.
to leading order for the flattened bubble case. We present explicit numerical results for the first few terms in the expansion for the case of an exponentially repulsive disjoining pressure, and analytic expressions for these terms in the limit of very short-range disjoining pressure forces. The results of this calculation are compared with recent work (Hodges, Jensen & Rallison, J. Fluid Mech., vol. 512, 2004, p. 95) where disjoining pressure is neglected and hydrodynamic pressure is balanced against buoyancy and Laplace forces. The limits of validity of this linear drag theory are also presented.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 11
- Cited by

