Article contents
The dominant mechanisms for each regime of secondary flows in horizontal particle-laden pipe flows
Published online by Cambridge University Press: 23 September 2022
Abstract
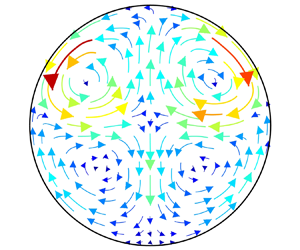
Numerical simulations have been conducted to identify the dominant mechanism responsible for driving secondary flow motions in horizontal particle-laden pipe flows, based on an analysis of the forces acting on each phase. A four-way coupling Euler–Lagrangian approach was employed, using direct numerical simulations for the gas phase and Lagrangian particle tracking to account for the drag, gravitational and lift forces, together with the interactions that occur for both particle–wall and inter-particle collisions. The four different flow regimes, which had been identified previously as depending on various combinations of flow parameters and are characterised by the secondary flow structures of both the fluid and particle phases, were identified via varying the mass loading alone from  $\varPhi _m=0.4$ to
$\varPhi _m=0.4$ to  $\varPhi _m=1.8$. The distribution of the divergence of Reynolds stresses was used to help characterise the classes of the secondary fluid flow. This shows that secondary fluid flows of both the first and second kinds can either exist separately or co-exist in such flows. The forces exerted on the fluid phase by the pressure gradient and fluid–particle interactions were examined qualitatively and quantitatively to identify their contribution to the secondary fluid flow motions. A similar study was also applied to the drag, lift and gravitational forces exerted on the particle phase for the secondary particle flow motions. These were found to explain the secondary flows of both the fluid and particle phases with regard to both the flow direction and magnitude, together with the interaction between the two phases.
$\varPhi _m=1.8$. The distribution of the divergence of Reynolds stresses was used to help characterise the classes of the secondary fluid flow. This shows that secondary fluid flows of both the first and second kinds can either exist separately or co-exist in such flows. The forces exerted on the fluid phase by the pressure gradient and fluid–particle interactions were examined qualitatively and quantitatively to identify their contribution to the secondary fluid flow motions. A similar study was also applied to the drag, lift and gravitational forces exerted on the particle phase for the secondary particle flow motions. These were found to explain the secondary flows of both the fluid and particle phases with regard to both the flow direction and magnitude, together with the interaction between the two phases.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by


