Hostname: page-component-5b777bbd6c-skqgd Total loading time: 0 Render date: 2025-06-24T02:00:29.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation and breakup of a ferrofluid compound droplet migrating in a microchannel under a magnetic field: a phase-field-based multiple-relaxation time lattice Boltzmann study

Published online by Cambridge University Press:  23 June 2025

Parham Poureslami Open the ORCID record for Parham Poureslami [Opens in a new window] ,
Mohammad Majidi ,
Javad Ranjbar Kermani Open the ORCID record for Javad Ranjbar Kermani [Opens in a new window]  and
Mohamad Ali Bijarchi Open the ORCID record for Mohamad Ali Bijarchi [Opens in a new window]
Parham Poureslami
Affiliation:
Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran
Mohammad Majidi
Affiliation:
Department of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran
Javad Ranjbar Kermani
Affiliation:
Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran
Mohamad Ali Bijarchi*
Affiliation:
Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran
*
Corresponding author: Mohamad Ali Bijarchi, bijarchi@sharif.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

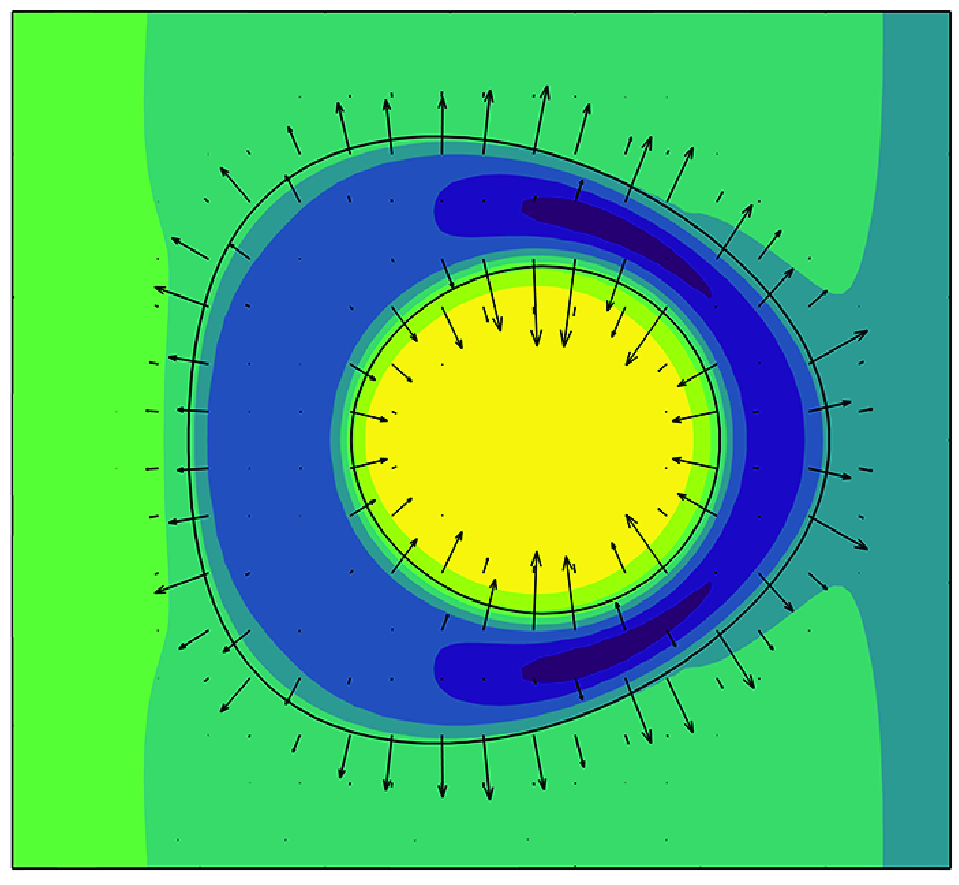
Though ubiquitous in many engineering applications, including drug delivery, the compound droplet hydrodynamics in confined geometries have been barely surveyed. For the first time, this study thoroughly investigates the hydrodynamics of a ferrofluid compound droplet (FCD) during its migration in a microchannel under the presence of a pressure-driven flow and a uniform external magnetic field (UEMF) to manipulate its morphology and retard its breakup. Finite difference and phase-field multiple-relaxation time lattice Boltzmann approaches are coupled to determine the magnetic field and ternary flow system, respectively. First, the influence of the magnetic Bond number (${Bo}_m$) on the FCD morphology is explored depending on whether the core or shell is ferrofluid when the UEMF is applied along $\alpha =0^\circ$ and $\alpha =90^\circ$ relative to the fluid flow. It is ascertained that imposing the UEMF at $\alpha =0^\circ$ when the shell is ferrofluid can postpone the breakup. Intriguingly, when the core is ferrofluid, strengthening the UEMF enlarges the shell deformation. Afterwards, the effects of the capillary number (${Ca}$), density ratio, viscosity ratio, radius ratio and surface tension coefficients are scrutinised on the FCD deformation and breakup. The results indicate that augmenting the core-to-shell viscosity and density ratios accelerates the breakup process. Additionally, surface tension between the core and shell suppresses the core deformation. Moreover, increasing the ${Ca}$ intensifies the viscous drag force exerted on the shell, flattening its rear side, which causes a triangular-like configuration. Ultimately, by varying ${Bo}_m$ and ${Ca}$, five distinct regimes are observed, whose regime map is established.

JFM classification

Drops and Bubbles: Drops and Bubbles Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A37
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abadi, R.H.H., Fakhari, A. & Rahimian, M.H. 2018 a Numerical simulation of three-component multiphase flows at high density and viscosity ratios using lattice Boltzmann methods. Phys. Rev. E 97 (3), 033312.10.1103/PhysRevE.97.033312CrossRefGoogle Scholar
Abadi, R.H.H., Rahimian, M.H. & Fakhari, A. 2018 b Conservative phase-field lattice-Boltzmann model for ternary fluids. J. Comput. Phys. 374, 668–691.10.1016/j.jcp.2018.07.045CrossRefGoogle Scholar
Abdo, R.F., Abicalil, V.G., Cunha, L.H.P. & Oliveira, T.F. 2023 On the rheology and magnetization of dilute magnetic emulsions under small amplitude oscillatory shear. J. Fluid Mech. 955, A3.10.1017/jfm.2022.1019CrossRefGoogle Scholar
Aboutalebi, M., Bijarchi, M.A., Shafii, M.B. & Kazemzadeh Hannani, S. 2018 Numerical investigation on splitting of ferrofluid microdroplets in T-junctions using an asymmetric magnetic field with proposed correlation. J. Magn. Magn. Mater. 447, 139–149.10.1016/j.jmmm.2017.09.053CrossRefGoogle Scholar
Behera, N., Poddar, A. & Chakraborty, S. 2023 Eccentricity-induced dielectrophoretic migration of a compound drop in a uniform external electric field. J. Fluid Mech. 963, A17.10.1017/jfm.2023.339CrossRefGoogle Scholar
Benther, J.D., Wilson, B., Petrini, P.A., Lappas, P. & Rosengarten, G. 2023 Ferrofluid droplet impingement cooling of modified surfaces under the influence of a magnetic field. Intl J. Heat Mass Transfer 215, 124370.10.1016/j.ijheatmasstransfer.2023.124370CrossRefGoogle Scholar
Bijarchi, M.A., Favakeh, A., Alborzi, S. & Shafii, M.B. 2021 Experimental investigation of on-demand ferrofluid droplet generation in microfluidics using a Pulse-Width Modulation magnetic field with proposed correlation. Sensors Actuat. B: Chem. 329, 129274.10.1016/j.snb.2020.129274CrossRefGoogle Scholar
Bijarchi, M.A., Favakeh, A., Sedighi, E. & Shafii, M.B. 2020 Ferrofluid droplet manipulation using an adjustable alternating magnetic field. Sensors Actuat. A: Phys. 301, 111753.10.1016/j.sna.2019.111753CrossRefGoogle Scholar
Bijarchi, M.A., Yaghoobi, M., Favakeh, A. & Shafii, M.B. 2022 On-demand ferrofluid droplet formation with non-linear magnetic permeability in the presence of high non-uniform magnetic fields. Sci. Rep.-UK 12 (1), 10868.10.1038/s41598-022-14624-wCrossRefGoogle ScholarPubMed
Borthakur, M.P., Biswas, G. & Bandyopadhyay, D. 2018 Dynamics of deformation and pinch-off of a migrating compound droplet in a tube. Phys. Rev. E 97 (4), 043112.10.1103/PhysRevE.97.043112CrossRefGoogle ScholarPubMed
Boyer, F. & Lapuerta, C. 2006 Study of a three component Cahn-Hilliard flow model. ESAIM: Math. Modell. Numer. Anal. 40 (4), 653–687.10.1051/m2an:2006028CrossRefGoogle Scholar
Boyer, F., Lapuerta, C., Minjeaud, S., Piar, B. & Quintard, M. 2010 Cahn–hilliard/Navier–Stokes model for the simulation of three-phase flows. Trans. Porous Med. 82 (3), 463–483.10.1007/s11242-009-9408-zCrossRefGoogle Scholar
Bracco, C., Giannelli, C., Reali, A., Torre, M. & Vázquez, R. 2023 Adaptive isogeometric phase-field modeling of the Cahn–Hilliard equation: Suitably graded hierarchical refinement and coarsening on multi-patch geometries. Comput. Meth. Appl. Mech. Engng 417, 116355. arXiv preprint arXiv: 2306.07112.10.1016/j.cma.2023.116355CrossRefGoogle Scholar
Che, Z., Yap, Y.F. & Wang, T. 2018 Flow structure of compound droplets moving in microchannels. Phys. Fluids 30 (1), 012114.10.1063/1.5008908CrossRefGoogle Scholar
Chen, H., Li, J., Shum, H.C., Stone, H.A. & Weitz, D.A. 2011 Breakup of double emulsions in constrictions. Soft Matter 7 (6), 2345–2347.10.1039/c0sm01100bCrossRefGoogle Scholar
Chen, S., Martinez, D. & Mei, R. 1996 On boundary conditions in lattice Boltzmann methods. Phys. Fluids 8 (9), 2527–2536.10.1063/1.869035CrossRefGoogle Scholar
Chen, Y., Liu, X. & Shi, M. 2013 Hydrodynamics of double emulsion droplet in shear flow. Appl. Phys. Lett. 102 (5), 051609.10.1063/1.4789865CrossRefGoogle Scholar
Chiu, P.-H. & Lin, Y.-T. 2011 A conservative phase field method for solving incompressible two-phase flows. J. Comput. Phys. 230 (1), 185–204.10.1016/j.jcp.2010.09.021CrossRefGoogle Scholar
Fakhari, A. & Lee, T. 2013 Multiple-relaxation-time lattice Boltzmann method for immiscible fluids at high Reynolds numbers. Phys. Rev. E 87 (2), 023304.10.1103/PhysRevE.87.023304CrossRefGoogle ScholarPubMed
Fakhari, A., Mitchell, T., Leonardi, C. & Bolster, D. 2017 Improved locality of the phase-field lattice-Boltzmann model for immiscible fluids at high density ratios. Phys. Rev. E 96 (5), 053301.10.1103/PhysRevE.96.053301CrossRefGoogle ScholarPubMed
Guilherme, A.L., Siqueira, I.R., Cunha, L.H.P., Thompson, R.L. & Oliveira, T.F. 2023 Ferrofluid droplets in planar extensional flows: droplet shape and magnetization reveal novel rheological signatures of ferrofluid emulsions. Phys. Rev. Fluids 8 (6), 063601.10.1103/PhysRevFluids.8.063601CrossRefGoogle Scholar
Guzowski, J., Korczyk, P.M., Jakiela, S. & Garstecki, P. 2012 The structure and stability of multiple micro-droplets. Soft Matter 8 (27), 7269–7278.10.1039/c2sm25838bCrossRefGoogle Scholar
Hao, G., Li, L., Gao, W., Liu, X. & Chen, Y. 2023 Electric-field-controlled deformation and spheroidization of compound droplet in an extensional flow. Intl J. Multiphase Flow 168, 104559.10.1016/j.ijmultiphaseflow.2023.104559CrossRefGoogle Scholar
Hassan, M.R. & Wang, C. 2019 Magnetic field induced ferrofluid droplet breakup in a simple shear flow at a low reynolds number. Phys. Fluids 31 (12), 127104.10.1063/1.5124134CrossRefGoogle Scholar
Heidari, F., Jafari, S.M., Ziaiifar, A.M. & Malekjani, N. 2022 Stability and release mechanisms of double emulsions loaded with bioactive compounds; a critical review. Adv. Colloid Interface 299, 102567.10.1016/j.cis.2021.102567CrossRefGoogle ScholarPubMed
Ho, N.X. & Vu, T.V. 2020 Numerical simulation of the deformation and breakup of a two-core compound droplet in an axisymmetric T-junction channel. Intl J. Heat Fluid Flow 86, 108702.10.1016/j.ijheatfluidflow.2020.108702CrossRefGoogle Scholar
Hua, H., Shin, J. & Kim, J. 2014 Dynamics of a compound droplet in shear flow. Intl J. Heat Fluid Flow 50, 63–71.10.1016/j.ijheatfluidflow.2014.05.007CrossRefGoogle Scholar
Huang, X., Saadat, M., Bijarchi, M.A. & Shafii, M.B. 2023 Ferrofluid double emulsion generation and manipulation under magnetic fields. Chem. Engng Sci. 270, 118519.10.1016/j.ces.2023.118519CrossRefGoogle Scholar
Kole, M. & Khandekar, S. 2021 Engineering applications of ferrofluids: A review. J. Magn. Magn. Mater. 537, 168222.10.1016/j.jmmm.2021.168222CrossRefGoogle Scholar
Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G. & Viggen, E.M. 2017 The Lattice Boltzmann Method. Springer International Publishing. 10 (978-3), 4-15.10.1007/978-3-319-44649-3CrossRefGoogle Scholar
Kumar, A. 2004 Isotropic finite-differences. J. Comput. Phys. 201 (1), 109–118.10.1016/j.jcp.2004.05.005CrossRefGoogle Scholar
Kumar, A., Kaur, R., Kumar, V., Kumar, S., Gehlot, R. & Aggarwal, P. 2022 New Insights into Water-in-Oil-in-Water (w/o/w) Double Emulsions: Properties, Fabrication, Instability Mechanism, and Food Applications. Trends in Food Science & Technology.Google Scholar
Lallemand, P. & Luo, L.-S. 2000 Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 61 (6), 6546–6562.10.1103/PhysRevE.61.6546CrossRefGoogle ScholarPubMed
Li, J., Chen, H. & Stone, H.A. 2011 Breakup of double emulsion droplets in a tapered nozzle. Langmuir 27 (8), 4324–4327.10.1021/la200473hCrossRefGoogle Scholar
Li, Y., Jeong, D., Kim, H., Lee, C. & Kim, J. 2019 Comparison study on the different dynamics between the Allen–Cahn and the Cahn–Hilliard equations. Comput. Maths Appl. 77 (2), 311–322.10.1016/j.camwa.2018.09.034CrossRefGoogle Scholar
Liu, H., Lu, Y., Li, S., Yu, Y. & Sahu, K.C. 2021 Deformation and breakup of a compound droplet in three-dimensional oscillatory shear flow. Intl J. Multiphase Flow 134, 103472.10.1016/j.ijmultiphaseflow.2020.103472CrossRefGoogle Scholar
Liu, J., Tan, S.-H., Yap, Y.F., Ng, M.Y. & Nguyen, N.-T. 2011 Numerical and experimental investigations of the formation process of ferrofluid droplets. Microfluid. Nanofluid. 11 (2), 177–187.10.1007/s10404-011-0784-7CrossRefGoogle Scholar
Loewenberg, M. & Hinch, E.J. 1996 Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 321, 395–419.10.1017/S002211209600777XCrossRefGoogle Scholar
Luo, Z.Y., He, L. & Bai, B.F. 2015 Deformation of spherical compound capsules in simple shear flow. J. Fluid Mech. 775, 77–104.10.1017/jfm.2015.286CrossRefGoogle Scholar
Ma, Z., Zhang, S., Wang, B., Liu, Q. & Chen, X. 2023 Deformation characteristics of compound droplets with different morphologies during transport in a microchannel. Phys. Fluids 35 (4), 042003.Google Scholar
Majidi, M., Bijarchi, M.A., Arani, A.G., Rahimian, M.H. & Shafii, M.B. 2022 Magnetic field-induced control of a compound ferrofluid droplet deformation and breakup in shear flow using a hybrid lattice Boltzmann-finite difference method. Intl J. Multiphase Flow 146, 103846.10.1016/j.ijmultiphaseflow.2021.103846CrossRefGoogle Scholar
Mandal, S., Ghosh, U. & Chakraborty, S. 2016 Effect of surfactant on motion and deformation of compound droplets in arbitrary unbounded Stokes flows. J. Fluid Mech. 803, 200–249.10.1017/jfm.2016.497CrossRefGoogle Scholar
Mandal, S., Sinha, S., Bandopadhyay, A. & Chakraborty, S. 2018 Drop deformation and emulsion rheology under the combined influence of uniform electric field and linear flow. J. Fluid Mech. 841, 408–433.10.1017/jfm.2017.897CrossRefGoogle Scholar
McNamara, G.R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61 (20), 2332–2335.10.1103/PhysRevLett.61.2332CrossRefGoogle ScholarPubMed
Mitchell, T.R., Majidi, M., Rahimian, M.H. & Leonardi, C.R. 2021 Computational modeling of three-dimensional thermocapillary flow of recalcitrant bubbles using a coupled lattice Boltzmann-finite difference method. Phys. Fluids 33 (3), 032108.10.1063/5.0038171CrossRefGoogle Scholar
Nguyen, C.T., Vu, H.V., Vu, T.V., Truong, T.V., Ho, N.X., Pham, B.D., Nguyen, H.D. & Nguyen, V.T. 2021 Numerical analysis of deformation and breakup of a compound droplet in microchannels. Eur. J. Mech.-B/Fluids 88, 135–147.10.1016/j.euromechflu.2021.03.005CrossRefGoogle Scholar
Obeid, M.A., Ogah, C.A., Ogah, C.O., Ajala, O.S., Aldea, M.R., Gray, A.I., Igoli, J.I. & Ferro, V.A. 2023 Formulation and evaluation of nanosized hippadine-loaded niosome: extraction and isolation, physicochemical properties, and in vitro cytotoxicity against human ovarian and skin cancer cell lines. J. Drug Deliv. Sci. Tech. 87, 104766.10.1016/j.jddst.2023.104766CrossRefGoogle Scholar
Philip, J. 2022 Magnetic nanofluids: recent advances, applications, challenges, and future directions. Adv. Colloid Interface Sci. 311, 102810.10.1016/j.cis.2022.102810CrossRefGoogle ScholarPubMed
Poureslami, P., Siavashi, M., Moghimi, H. & Hosseini, M. 2021 Pore-scale convection-conduction heat transfer and fluid flow in open-cell metal foams: A three-dimensional multiple-relaxation time lattice Boltzmann (MRT-LBM) solution. Intl Commun. Heat Mass 126, 105465.10.1016/j.icheatmasstransfer.2021.105465CrossRefGoogle Scholar
Qu, X. & Wang, Y. 2012 Dynamics of concentric and eccentric compound droplets suspended in extensional flows. Phys. Fluids 24 (12), 123302.10.1063/1.4770294CrossRefGoogle Scholar
Santra, S., Das, S. & Chakraborty, S. 2019 Electric field-induced pinch-off of a compound droplet in Poiseuille flow. Phys. Fluids 31 (6), 062004.10.1063/1.5094948CrossRefGoogle Scholar
Santra, S., Das, S. & Chakraborty, S. 2020 a Electrically modulated dynamics of a compound droplet in a confined microfluidic environment. J. Fluid Mech. 882, A23.10.1017/jfm.2019.810CrossRefGoogle Scholar
Santra, S., Panigrahi, D.P., Das, S. & Chakraborty, S. 2020 b Shape evolution of compound droplet in combined presence of electric field and extensional flow. Phys. Rev. Fluids 5 (6), 063602.10.1103/PhysRevFluids.5.063602CrossRefGoogle Scholar
Sattari, A., Tasnim, N., Hanafizadeh, P. & Hoorfar, M. 2021 Motion and deformation of migrating compound droplets in shear-thinning fluids in a microcapillary tube. Phys. Fluids 33 (5), 053106.10.1063/5.0045994CrossRefGoogle Scholar
Shah, R.K. & Khandekar, S. 2022 On-demand augmentation in heat transfer of Taylor bubble flows using ferrofluids. Appl. Therm. Engng 205, 118058.10.1016/j.applthermaleng.2022.118058CrossRefGoogle Scholar
Singeetham, P.K., Chaithanya, K.V.S. & Thampi, S.P. 2021 Dilute dispersion of compound particles: deformation dynamics and rheology. J. Fluid Mech. 917, A2.10.1017/jfm.2021.233CrossRefGoogle Scholar
Sun, Y. & Beckermann, C. 2007 Sharp interface tracking using the phase-field equation. J. Comput. Phys. 220 (2), 626–653.10.1016/j.jcp.2006.05.025CrossRefGoogle Scholar
Gurumurthy Thammanna, V. & Pushpavanam, S. 2020 Hydrodynamics of a compound drop in plane poiseuille flow. Phys. Fluids 32 (7), 072003.10.1063/5.0009401CrossRefGoogle Scholar
Vu, H.V., Vu, T.V., Pham, B.D., Nguyen, H.D., Nguyen, V.T., Phan, H.T. & Nguyen, C.T. 2023 Deformation of a compound droplet in a wavy constricted channel. J. Mech. Sci. Technol. 37 (1), 191–202.10.1007/s12206-022-1220-5CrossRefGoogle Scholar
Vu, T.-V., Vu, T.V. & Bui, D.T. 2019 a Numerical study of deformation and breakup of a multi-core compound droplet in simple shear flow. Intl J. Heat Mass Transfer 131, 1083–1094.10.1016/j.ijheatmasstransfer.2018.11.131CrossRefGoogle Scholar
Vu, T.-V., Vu, T.V., Nguyen, C.T. & Pham, P.H. 2019 b Deformation and breakup of a double-core compound droplet in an axisymmetric channel. Intl J. Heat Mass Transfer 135, 796–810.10.1016/j.ijheatmasstransfer.2019.02.032CrossRefGoogle Scholar
Wang, K., Xia, Y.-C. & Li, Z.-Y. 2023 A phase-field Lattice Boltzmann method for liquid-vapor phase change problems based on conservative Allen-Cahn equation and adaptive treegrid. Comput. Fluids 264, 105973.10.1016/j.compfluid.2023.105973CrossRefGoogle Scholar
Wang, N., Semprebon, C., Liu, H., Zhang, C. & Kusumaatmaja, H. 2020 Modelling double emulsion formation in planar flow-focusing microchannels. J. Fluid Mech. 895, A22.10.1017/jfm.2020.299CrossRefGoogle Scholar
Wei, W., Chen, F., Qiu, Y., Zhang, L., Gao, J., Wu, T., Wang, P., Zhang, M. & Zhu, Q. 2023 Co-encapsulation of collagen peptide and astaxanthin in WG/OG/W double emulsions-filled alginate hydrogel beads: Fabrication, characterization and digestion behaviors. J. Colloid Interface Sci. 651, 159–171.10.1016/j.jcis.2023.07.201CrossRefGoogle Scholar
Wu, J., Gao, C., Sun, D., Yang, L., Ye, B., Wang, T. & Zhou, P. 2023 a Thermally mediated double emulsion droplets formation in a six-way junction microfluidic device. Colloid. Surfaces A: Physicochem. Engng Aspects 661, 130961.10.1016/j.colsurfa.2023.130961CrossRefGoogle Scholar
Wu, L., Qian, J., Liu, X., Wu, S., Yu, C. & Liu, X. 2023 b Numerical modelling for the droplets formation in microfluidics-a review. Microgr. Sci. Technol. 35 (3), 1–21.10.1007/s12217-023-10053-0CrossRefGoogle Scholar
Zhang, P., Xu, L., Chen, H. & Abate, A.R. 2023 a Flow cytometric printing of double emulsions into open droplet arrays. Lab Chip 23 (10), 2371–2377.10.1039/D3LC00151BCrossRefGoogle ScholarPubMed
Zhang, S.-T., Niu, X.-D., Li, Q.-P., Khan, A., Hu, Y. & Li, D.-C. 2023 b A numerical investigation on the deformation of ferrofluid droplets. Phys. Fluids 35 (1), 012102.10.1063/5.0131884CrossRefGoogle Scholar
Zou, Q. & He, X. 1997 On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 9 (6), 1591–1598.10.1063/1.869307CrossRefGoogle Scholar
Zu, Y.Q. & He, S. 2013 Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts. Phys. Rev. E 87 (4), 043301.10.1103/PhysRevE.87.043301CrossRefGoogle ScholarPubMed
Supplementary material: File

Poureslami et al. supplementary material

Poureslami et al. supplementary material
Download Poureslami et al. supplementary material(File)
File 1.5 MB