Hostname: page-component-65f69f4695-xtrld Total loading time: 0 Render date: 2025-06-27T05:39:47.509Z Has data issue: false hasContentIssue false
  • English
  • Français

A deep learning approach to wall-shear stress quantification: from numerical training to zero-shot experimental application

Published online by Cambridge University Press:  25 June 2025

Esther Lagemann Open the ORCID record for Esther Lagemann [Opens in a new window] ,
Julia Roeb Open the ORCID record for Julia Roeb [Opens in a new window] ,
Steven L. Brunton Open the ORCID record for Steven L. Brunton [Opens in a new window]  and
Christian Lagemann Open the ORCID record for Christian Lagemann [Opens in a new window]
Esther Lagemann*
Affiliation:
AI Institute in Dynamic Systems, Department of Mechanical Engineering, University of Washington, Seattle, WA 98195, USA
Julia Roeb
Affiliation:
Engler-Bunte-Institut, Simulation of Reacting Thermo-Fluid Systems, Karlsruhe Institute for Technology, Engler-Bunte-Ring 7, Karlsruhe 76131, Germany
Steven L. Brunton
Affiliation:
AI Institute in Dynamic Systems, Department of Mechanical Engineering, University of Washington, Seattle, WA 98195, USA
Christian Lagemann
Affiliation:
AI Institute in Dynamic Systems, Department of Mechanical Engineering, University of Washington, Seattle, WA 98195, USA
*
Corresponding author: Esther Lagemann, elage@uw.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

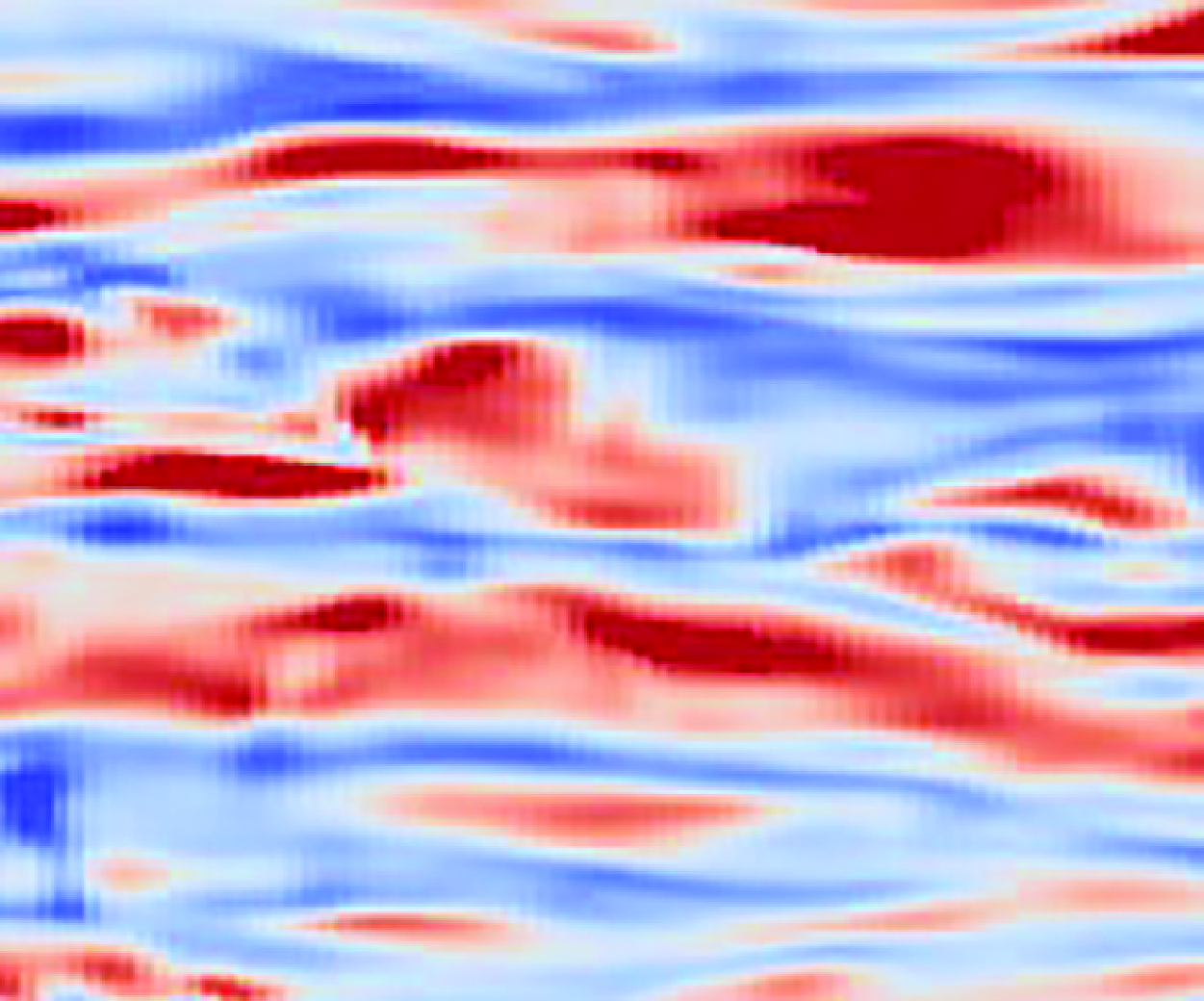
The accurate quantification of wall-shear stress dynamics is of substantial importance for various applications in fundamental and applied research, spanning areas from human health to aircraft design and optimization. Despite significant progress in experimental measurement techniques and postprocessing algorithms, temporally resolved wall-shear stress fields with adequate spatial resolution and within a suitable spatial domain remain an elusive goal. Furthermore, there is a systematic lack of universal models that can accurately replicate the instantaneous wall-shear stress dynamics in numerical simulations of multiscale systems where direct numerical simulations (DNSs) are prohibitively expensive. To address these gaps, we introduce a deep learning architecture that ingests wall-parallel streamwise velocity fields at $y^+ \approx 3.9 \sqrt {Re_\tau }$ of turbulent wall-bounded flows and outputs the corresponding two-dimensional streamwise wall-shear stress fields with identical spatial resolution and domain size. From a physical perspective, our framework acts as a surrogate model encapsulating the various mechanisms through which highly energetic outer-layer flow structures influence the governing wall-shear stress dynamics. The network is trained in a supervised fashion on a unified dataset comprising DNSs of statistically one-dimensional turbulent channel and spatially developing turbulent boundary layer flows at friction Reynolds numbers ranging from $390$ to $1500$. We demonstrate a zero-shot applicability to experimental velocity fields obtained from particle image velocimetry measurements and verify the physical accuracy of the wall-shear stress estimates with synchronized wall-shear stress measurements using the micro-pillar shear-stress sensor for Reynolds numbers up to $2000$. In summary, the presented framework lays the groundwork for extracting inaccessible experimental wall-shear stress information from readily available velocity measurements and thus, facilitates advancements in a variety of experimental applications.

JFM classification

Mathematical Foundations: Machine learning Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1014 , 10 July 2025 , A1
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adamo, L. et al. 2009 Biomechanical forces promote embryonic haematopoiesis. Nature 459 (7250), 1131–1135.CrossRefGoogle ScholarPubMed
Agostini, L. & Leschziner, M.A. 2014 On the influence of outer large-scale structures on near-wall turbulence in channel flow. Phys. Fluids 26 (7), 075107.10.1063/1.4890745CrossRefGoogle Scholar
Albers, M., Meysonnat, P.S., Fernex, D., Semaan, R., Noack, B.R. & Schröder, W. 2020 Drag reduction and energy saving by spanwise traveling transversal surface waves for flat plate flow. Flow Turbul. Combust. 105 (1), 125–157.10.1007/s10494-020-00110-8CrossRefGoogle Scholar
Arzani, A. & Dawson, S.T.M. 2021 Data-driven cardiovascular flow modelling: examples and opportunities. J. R. Soc. Interface 18 (175), 20200802.10.1098/rsif.2020.0802CrossRefGoogle ScholarPubMed
Baars, W.J., Talluru, K.M., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluids 56 (10), 188.10.1007/s00348-015-2058-8CrossRefGoogle Scholar
Balasubramanian, A.G., Guastoni, L., Schlatter, P., Azizpour, H. & Vinuesa, R. 2023 Predicting the wall-shear stress and wall pressure through convolutional neural networks. Intl J. Heat Fluid Flow 103, 109200.10.1016/j.ijheatfluidflow.2023.109200CrossRefGoogle Scholar
Bellien, J., Iacob, M., Richard, V., Wils, J., Le Cam-Duchez, V. & Joannidès, R. 2021 Evidence for wall shear stress-dependent t-PA release in human conduit arteries: role of endothelial factors and impact of high blood pressure. Hypertens. Res. 44 (3), 310–317.10.1038/s41440-020-00554-5CrossRefGoogle Scholar
Brunton, S.L., Noack, B.R. & Koumoutsakos, P. 2020 Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52 (1), 477–508.10.1146/annurev-fluid-010719-060214CrossRefGoogle Scholar
Brunton, S.L., Proctor, J.L. & Kutz, J.N. 2016 Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113 (15), 3932–3937.10.1073/pnas.1517384113CrossRefGoogle ScholarPubMed
Eivazi, H., Wang, Y. & Vinuesa, R. 2024 Physics-informed deep-learning applications to experimental fluid mechanics. Meas. Sci. Technol. 35 (7), 075303.CrossRefGoogle Scholar
Erichson, N.B., Mathelin, L., Yao, Z., Brunton, S.L., Mahoney, M.W. & Kutz, J.N. 2020 Shallow neural networks for fluid flow reconstruction with limited sensors. Proc. R. Soc. Lond. A 476 (2238), 20200097.Google ScholarPubMed
Ferdian, E., Dubowitz, D.J., Mauger, C.A., Wang, A. & Young, A.A. 2022 WSSNet: aortic wall shear stress estimation using deep learning on 4D flow MRI. Front. Cardiovasc. Med. 8, 769927.10.3389/fcvm.2021.769927CrossRefGoogle ScholarPubMed
Fernex, D., Semaan, R., Albers, M., Meysonnat, P.S., Schröder, W. & Noack, B.R. 2020 Actuation response model from sparse data for wall turbulence drag reduction. Phys. Rev. Fluids 5 (7), 073901.10.1103/PhysRevFluids.5.073901CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J.P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Garrido-Oliver, J. et al. 2022 Machine learning for the automatic assessment of aortic rotational flow and wall shear stress from 4D flow cardiac magnetic resonance imaging. Eur. Radiol. 32 (10), 7117–7127.10.1007/s00330-022-09068-9CrossRefGoogle ScholarPubMed
Geurts, K.J., Nottebrock, B. & Schröder, W. 2014 Wall-shear stress measurements in an adverse pressure gradient turbulent boundary layer. In 7th AIAA Flow Control Conference, pp. 2098. AIAA AVIATION Forum.Google Scholar
Gharleghi, R., Sowmya, A. & Beier, S. 2022 Transient wall shear stress estimation in coronary bifurcations using convolutional neural networks. Comput. Meth. Prog. Bio. 225, 107013.10.1016/j.cmpb.2022.107013CrossRefGoogle ScholarPubMed
Graham, J. et al. 2016 A web services accessible database of turbulent channel flow and its use for testing a new integral wall model for les. J. Turbul. 17 (2), 181–215.10.1080/14685248.2015.1088656CrossRefGoogle Scholar
Große, S. & Schröder, W. 2008 Dynamic wall-shear stress measurements in turbulent pipe flow using the micro-pillar sensor MPS3. Intl J. Heat Fluid Flow 29 (3), 830–840.10.1016/j.ijheatfluidflow.2008.01.008CrossRefGoogle Scholar
Große, S. & Schröder, W. 2009 Wall-shear stress patterns of coherent structures in turbulent duct flow. J. Fluid Mech. 633, 147–158.CrossRefGoogle Scholar
Güemes, A., Discetti, S., Ianiro, A., Sirmacek, B., Azizpour, H. & Vinuesa, R. 2021 From coarse wall measurements to turbulent velocity fields through deep learning. Phys. Fluids 33 (7), 075121.10.1063/5.0058346CrossRefGoogle Scholar
He, K., Zhang, X., Ren, S. & Sun, J. 2016 Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.10.1017/S0022112091002033CrossRefGoogle Scholar
Lagemann, C., Lagemann, K., Mukherjee, S. & Schröder, W. 2021 Deep recurrent optical flow learning for particle image velocimetry data. Nat. Mach. Intell. 3 (7), 641–651.10.1038/s42256-021-00369-0CrossRefGoogle Scholar
Lagemann, C., Lagemann, K., Mukherjee, S. & Schröder, W. 2022 Generalization of deep recurrent optical flow estimation for particle-image velocimetry data. Meas. Sci. Technol. 33 (9), 094003.10.1088/1361-6501/ac73dbCrossRefGoogle Scholar
Lagemann, C., Lagemann, K., Mukherjee, S. & Schröder, W. 2024 a Challenges of deep unsupervised optical flow estimation for particle-image velocimetry data. Exp. Fluids 65 (3), 1–18.10.1007/s00348-024-03768-2CrossRefGoogle Scholar
Lagemann, E., Albers, M., Lagemann, C. & Schröder, W. 2024 Impact of Reynolds number on the drag reduction mechanism of spanwise travelling surface waves. Flow Turbul. Combust. 113, 27–40.CrossRefGoogle Scholar
Lagemann, E., Brunton, S.L. & Lagemann, C. 2024 b Uncovering wall-shear stress dynamics from neural-network enhanced fluid flow measurements. Proc. R. Soc. Lond. A 480 (2292), 20230798.Google Scholar
Lagemann, E., Brunton, S.L., Schröder, W. & Lagemann, C. 2024 c Towards extending the aircraft flight envelope by mitigating transonic airfoil buffet. Nat. Commun. 15 (1), 5020.10.1038/s41467-024-49361-3CrossRefGoogle ScholarPubMed
Lagemann, K., Lagemann, C. & Mukherjee, S. 2023 b Invariance-based learning of latent dynamics. In The Twelfth International Conference on Learning Representations.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.CrossRefGoogle Scholar
Liu, Y., Klaas, M. & Schröder, W. 2019 Measurements of the wall-shear stress distribution in turbulent channel flow using the micro-pillar shear stress sensor MPS3. Exp. Therm. Fluid Sci. 106, 171–182.CrossRefGoogle Scholar
Marquardt, P., Klaas, M. & Schröder, W. 2019 Experimental investigation of isoenergetic film-cooling flows with shock interaction. AIAA J. 57 (9), 3910–3923.10.2514/1.J058197CrossRefGoogle Scholar
Marquardt, P., Klaas, M. & Schröder, W. 2020 Experimental investigation of the turbulent Schmidt number in supersonic film cooling with shock interaction. Exp. Fluids 61 (7), 160.10.1007/s00348-020-02983-xCrossRefGoogle Scholar
Marusic, I., Baars, W.J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall turbulence. Phys. Rev. Fluids 2 (10), 100502.10.1103/PhysRevFluids.2.100502CrossRefGoogle Scholar
Marusic, I. & Heuer, W.D.C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.10.1103/PhysRevLett.99.114504CrossRefGoogle ScholarPubMed
Marusic, I., Mathis, R. & Hutchins, N. 2010 a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.10.1016/j.ijheatfluidflow.2010.01.005CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 b Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.10.1126/science.1188765CrossRefGoogle ScholarPubMed
Mäteling, E., Albers, M. & Schröder, W. 2023 How spanwise travelling transversal surface waves change the near-wall flow. J. Fluid Mech. 957, A30.CrossRefGoogle Scholar
Mäteling, E., Klaas, M. & Schröder, W. 2020 a Detection of small-scale/large-scale interactions in turbulent wall-bounded flows. Phys. Rev. Fluids 5 (11), 114610.10.1103/PhysRevFluids.5.114610CrossRefGoogle Scholar
Mäteling, E., Klaas, M. & Schröder, W. 2020 b Simultaneous stereo PIV and MPS3 wall-shear stress measurements in turbulent channel flow. Optics 1 (1), 40–51.10.3390/opt1010004CrossRefGoogle Scholar
Mäteling, E. & Schröder, W. 2022 a Analysis of spatiotemporal inner-outer large-scale interactions in turbulent channel flow by multivariate empirical mode decomposition. Phys. Rev. Fluids 7 (3), 034603.10.1103/PhysRevFluids.7.034603CrossRefGoogle Scholar
Mäteling, E. & Schröder, W. 2022 b Analysis of spatiotemporal inner-outer large-scale interactions in turbulent channel flow by multivariate empirical mode decomposition [code]. Phys. Rev. Fluids 7 (3), 034603.10.1103/PhysRevFluids.7.034603CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946CrossRefGoogle Scholar
Nottebrock, B., Klaas, M. & Schröder, W. 2012 Improvement of the measurement range of the micro-pillar shear-stress sensor MPS3. In 28th Aerodynamic Measurement Technology, Ground Testing, and Flight Testing Conference including the Aerospace T&E Days Forum, pp. 3011.Google Scholar
Örlü, R. & Vinuesa, R. 2020 Instantaneous wall-shear-stress measurements: advances and application to near-wall extreme events. Meas. Sci. Technol. 31 (11), 112001.10.1088/1361-6501/aba06fCrossRefGoogle Scholar
Pathikonda, G. & Christensen, K.T. 2019 Investigation of inner-outer interactions in a turbulent boundary layer using high-speed particle image velocimetry. Phys. Rev. Fluids 4 (3), 034607.10.1103/PhysRevFluids.4.034607CrossRefGoogle Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing, pp. 1–11.Google Scholar
Raffel, M., Willert, C.E., Scarano, F., Kähler, C.J., Wereley, S.T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer Nature: Springer International Publishing AG.10.1007/978-3-319-68852-7CrossRefGoogle Scholar
Raissi, M., Perdikaris, P. & Karniadakis, G.E. 2019 Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707.10.1016/j.jcp.2018.10.045CrossRefGoogle Scholar
Ricco, P., Skote, M. & Leschziner, M.A. 2021 A review of turbulent skin-friction drag reduction by near-wall transverse forcing. Prog. Aerosp. Sci. 123, 100713.10.1016/j.paerosci.2021.100713CrossRefGoogle Scholar
Ronneberger, O., Fischer, P. & Brox, T. 2015 U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pp. 234–241. Springer.Google Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M.K., Fan, Y., Hultmark, M. & Smits, A.J. 2018 Fully resolved measurements of turbulent boundary layer flows up to $Re_\tau \approx 20\,000$ . J. Fluid Mech. 851, 391–415.10.1017/jfm.2018.508CrossRefGoogle Scholar
Scharnowski, S. & Kähler, C.J. 2020 Particle image velocimetry - classical operating rules from today’s perspective. Opt. Laser. Engng 135, 106185.10.1016/j.optlaseng.2020.106185CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Shone, F., Ravikumar, N., Lassila, T., MacRaild, M., Wang, Y., Taylor, Z.A., Jimack, P., Dall’Armellina, E. & Frangi, A.F. 2023 Deep physics-informed super-resolution of cardiac 4D-flow MRI. In International Conference on Information Processing in Medical Imaging, pp. 511–522. Springer.Google Scholar
Su, B., Zhang, J.-M., Zou, H., Ghista, D., Le, T.T. & Chin, C. 2020 Generating wall shear stress for coronary artery in real-time using neural networks: feasibility and initial results based on idealized models. Comput. Biol. Med. 126, 104038.10.1016/j.compbiomed.2020.104038CrossRefGoogle ScholarPubMed
Suk, J., de Haan, P., Lippe, P., Brune, C. & Wolterink, J.M. 2021 Mesh convolutional neural networks for wall shear stress estimation in 3D artery models. In International Workshop On Statistical Atlases and Computational Models of the Heart, pp. 93–102. Springer.Google Scholar
Tzima, E., Irani-Tehrani, M., Kiosses, W.B., Dejana, E., Schultz, D.A., Engelhardt, B., Cao, G., DeLisser, H. & Schwartz, M.A. 2005 A mechanosensory complex that mediates the endothelial cell response to fluid shear stress. Nature 437 (7057), 426–431.CrossRefGoogle ScholarPubMed
Udrescu, S.-M., Tan, A., Feng, J., Neto, O., Wu, T. & Tegmark, M. 2020 AI Feynman 2.0: pareto-optimal symbolic regression exploiting graph modularity. Adv. Neural Inform. Proc. Syst. 33, 4860–4871.Google Scholar
Udrescu, S.-M. & Tegmark, M. 2020 AI Feynman: a physics-inspired method for symbolic regression. Sci. Adv. 6 (16), eaay2631.10.1126/sciadv.aay2631CrossRefGoogle ScholarPubMed
Vinuesa, R. & Brunton, S.L. 2022 Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2 (6), 358–366.10.1038/s43588-022-00264-7CrossRefGoogle ScholarPubMed
Vinuesa, R., Brunton, S.L. & McKeon, B.J. 2023 The transformative potential of machine learning for experiments in fluid mechanics. Nat. Rev. Phys. 5 (9), 536–545.10.1038/s42254-023-00622-yCrossRefGoogle Scholar
Zhou, G., Zhu, Y., Yin, Y., Su, M., Li, M. 2017 Association of wall shear stress with intracranial aneurysm rupture: systematic review and meta-analysis. Sci. Rep. UK 7 (1), 1–8.Google ScholarPubMed