Article contents
Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra
Published online by Cambridge University Press: 12 November 2019
Abstract
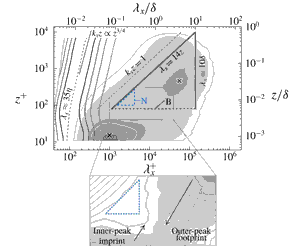
In wall-bounded turbulence, a multitude of coexisting turbulence structures form the streamwise velocity energy spectrum from the viscosity- to the inertia-dominated range of scales. Definite scaling-trends for streamwise spectra have remained empirically elusive, although a prominent school of thought stems from the works of Perry & Abell (J. Fluid Mech., vol. 79, 1977, pp. 785–799) and Perry et al. (J. Fluid Mech., vol. 165, 1986, pp. 163–199), which were greatly inspired by the attached-eddy hypothesis of Townsend (The Structure of Turbulent Shear Flow, Cambridge University Press, 1976). In this paper, we re-examine the turbulence kinetic energy of the streamwise velocity component in the context of the spectral decompositions of Perry and co-workers. Two universal spectral filters are derived via spectral coherence analysis of two-point velocity signals, spanning a Reynolds-number range  $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3})$ to
$Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3})$ to  $O(10^{6})$ and form the basis for our decomposition of the logarithmic-region turbulence into stochastically wall-detached and wall-attached portions of energy. The latter is composed of scales larger than a streamwise/wall-normal ratio of
$O(10^{6})$ and form the basis for our decomposition of the logarithmic-region turbulence into stochastically wall-detached and wall-attached portions of energy. The latter is composed of scales larger than a streamwise/wall-normal ratio of  $\unicode[STIX]{x1D706}_{x}/z\approx 14$. If the decomposition is accepted, a
$\unicode[STIX]{x1D706}_{x}/z\approx 14$. If the decomposition is accepted, a  $k_{x}^{-1}$ scaling region can only appear for
$k_{x}^{-1}$ scaling region can only appear for  $Re_{\unicode[STIX]{x1D70F}}\gtrsim 80\,000$, at a wall-normal position of
$Re_{\unicode[STIX]{x1D70F}}\gtrsim 80\,000$, at a wall-normal position of  $z^{+}=100$. Following Perry and co-workers, it is hypothesized that spectral contributions from turbulence structures other than attached eddies obscure a
$z^{+}=100$. Following Perry and co-workers, it is hypothesized that spectral contributions from turbulence structures other than attached eddies obscure a  $k_{x}^{-1}$ scaling. When accepting the idea of different spectral contributions it is furthermore shown that a broad outer-spectral peak is present even at low
$k_{x}^{-1}$ scaling. When accepting the idea of different spectral contributions it is furthermore shown that a broad outer-spectral peak is present even at low  $Re_{\unicode[STIX]{x1D70F}}$.
$Re_{\unicode[STIX]{x1D70F}}$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 72
- Cited by
Linked content
Please note that this article has a (1).

