Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Agudo, J. R.
Illigmann, C.
Luzi, G.
Laukart, A.
Delgado, A.
and
Wierschem, A.
2017.
Shear-induced incipient motion of a single sphere on uniform substrates at low particle Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 825,
Issue. ,
p.
284.
Salevan, J. C.
Clark, Abram H.
Shattuck, Mark D.
O'Hern, Corey S.
and
Ouellette, Nicholas T.
2017.
Determining the onset of hydrodynamic erosion in turbulent flow.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Kudrolli, Arshad
Ionkin, Nikolay
and
Panaitescu, Andreea
2017.
Headward growth and branching in subterranean channels.
Physical Review E,
Vol. 96,
Issue. 5,
Clark, Abram H.
Shattuck, Mark D.
Ouellette, Nicholas T.
and
O'Hern, Corey S.
2017.
Role of grain dynamics in determining the onset of sediment transport.
Physical Review Fluids,
Vol. 2,
Issue. 3,
Pähtz, Thomas
and
Durán, Orencio
2018.
The Cessation Threshold of Nonsuspended Sediment Transport Across Aeolian and Fluvial Environments.
Journal of Geophysical Research: Earth Surface,
Vol. 123,
Issue. 8,
p.
1638.
Campen, Sophie
Smith, Benjamin
and
Wong, Janet
2018.
Deposition of Asphaltene from Destabilized Dispersions in Heptane–Toluene.
Energy & Fuels,
Vol. 32,
Issue. 9,
p.
9159.
Allen, Benjamin
and
Kudrolli, Arshad
2018.
Granular bed consolidation, creep, and armoring under subcritical fluid flow.
Physical Review Fluids,
Vol. 3,
Issue. 7,
Balta, Samire
and
Smith, Frank T.
2018.
Fluid flow lifting a body from a solid surface.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 474,
Issue. 2219,
Maldonado, Sergio
and
de Almeida, Gustavo A. M.
2019.
Theoretical impulse threshold for particle dislodgement.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
893.
Brunier-Coulin, Florian
Cuéllar, Pablo
and
Philippe, Pierre
2020.
Generalized Shields criterion for weakly cohesive granular materials.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Topic, N.
Agudo, J.R.
Luzi, G.
Czech, F.
and
Wierschem, A.
2022.
Shear-induced motion of a bead on regular substrates at small particle Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Smith, Frank T.
and
Liu, Kevin
2022.
Three-dimensional evolution of body and fluid motion near a wall.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 6,
p.
969.
Liu, Qingsong
Yazar, Samire
and
Smith, Frank
2023.
On interaction between freely moving bodies and fluid in a channel flow.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 1,
p.
100413.
Henry, Christophe
Minier, Jean-Pierre
and
Brambilla, Sara
2023.
Particle resuspension: Challenges and perspectives for future models.
Physics Reports,
Vol. 1007,
Issue. ,
p.
1.
Keetels, Geert H.
Chauchat, Julien
and
Breugem, Wim-Paul
2023.
Role of turbulent kinetic energy modulation by particle–fluid interaction in sediment pick-up.
Journal of Fluid Mechanics,
Vol. 955,
Issue. ,
Yazar, Samire
Liu, Qingsong
and
Smith, Frank T.
2024.
Fluid flow past a freely moving body in a straight or distorted channel.
Theoretical and Computational Fluid Dynamics,
Vol. 38,
Issue. 1,
p.
89.
Shallcross, Gregory S.
Hoey, William A.
Anderson, John R.
Soares, Carlos
and
Cooper, Moogega
2024.
Modeling adhesion and aerodynamic removal of particles and spores from substrates.
Journal of Aerosol Science,
Vol. 176,
Issue. ,
p.
106294.
De Souza, E.
Ouchene, R.
and
Thomas, L.
2025.
Determination of hydrodynamic torques on an oblate spheroid in contact with a smooth surface in a linear shear flow.
Physics of Fluids,
Vol. 37,
Issue. 7,
Ouchene, Rafik
2025.
Contribution to the study of the dislodgment conditions of spheroids from a surface in fluid flow.
Physics of Fluids,
Vol. 37,
Issue. 2,
Xu, Jun
Wang, Fei
and
Vaughan, Bryce
2025.
CFD–DEM Analysis of Internal Soil Erosion Induced by Infiltration into Defective Buried Pipes.
Geosciences,
Vol. 15,
Issue. 7,
p.
253.
 $\dot{\unicode[STIX]{x1D6FE}_{c}}$ needed to dislodge a spherical particle resting on a surface with a model asperity in laminar and turbulent fluid flows. We have built a cone-plane experimental apparatus which enables measurement of
$\dot{\unicode[STIX]{x1D6FE}_{c}}$ needed to dislodge a spherical particle resting on a surface with a model asperity in laminar and turbulent fluid flows. We have built a cone-plane experimental apparatus which enables measurement of 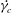 $\dot{\unicode[STIX]{x1D6FE}_{c}}$ over a wide range of particle Reynolds number
$\dot{\unicode[STIX]{x1D6FE}_{c}}$ over a wide range of particle Reynolds number 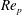 $Re_{p}$ from
$Re_{p}$ from 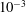 $10^{-3}$ to
$10^{-3}$ to 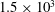 $1.5\times 10^{3}$ . The condition to dislodge the particle is found to be consistent with the torque balance condition after including the torque component due to drag about the particle centre. The data for
$1.5\times 10^{3}$ . The condition to dislodge the particle is found to be consistent with the torque balance condition after including the torque component due to drag about the particle centre. The data for 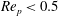 $Re_{p}<0.5$ are in good agreement with analytical calculations of the drag and lift coefficients in the
$Re_{p}<0.5$ are in good agreement with analytical calculations of the drag and lift coefficients in the 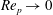 $Re_{p}\rightarrow 0$ limit. For higher
$Re_{p}\rightarrow 0$ limit. For higher 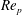 $Re_{p}$ , where analytical results are unavailable, the hydrodynamic coefficients are found to approach a constant for
$Re_{p}$ , where analytical results are unavailable, the hydrodynamic coefficients are found to approach a constant for 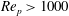 $Re_{p}>1000$ . We show that a linear combination of the hydrodynamic coefficients found in the viscous and inertial limits can describe the observed
$Re_{p}>1000$ . We show that a linear combination of the hydrodynamic coefficients found in the viscous and inertial limits can describe the observed 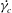 $\dot{\unicode[STIX]{x1D6FE}_{c}}$ as a function of the particle and fluid properties.
$\dot{\unicode[STIX]{x1D6FE}_{c}}$ as a function of the particle and fluid properties.

